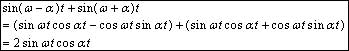平成17年度鹿児島県総合教育センターSPP事業教員研修 数学科学習指導案
|
数 学 科 学 習 指 導 案 日 時 平成○年○月○日( )第○校時 対象学級 ○年○組○人(男子○人女子○人) 学 校 名 鹿児島県立奄美高等学校 指 導 者 堂 薗 幸 夫 1 単元(題材)名 三角比 2 単元設定の理由 三角比は高校数学で初めて扱う教材である。本校では数学Ⅰのみしか履修しない。 数学Ⅰの時点では単なる計算に終始するが,その実奥深いものがある。 その一端を紹介し,数学の面白さを伝えたい。 3 生徒の実態 本校は専門高校であり,直接的に大学入試と連動しているわけではない。 数学に関しては専門教科と違い高い興味を示していない。また計算力も低い。 4 単元の目標 三角関数のグラフ(y=sinθ,y=cosθ)を描き,作る。 5 単元の指導計画 数学Ⅰで三角比が終了した時点で,その先を学習することは無い。 数学Ⅱの三角関数に一部入り,三角比の表からグラフを描く。 次に,実際にはさみで切りながら,正弦曲線を作ってみる。 写真などで実際の正弦曲線を提示する。 6 本時の実際(○/○) (1) 題材 正弦曲線の具現化 (2) 目標 数学は実生活に関係のない縁遠いものという印象を払拭し,身近な周りに存在するという ことを理解させる。 (3) 指導の実際
7 評価(一人一人の生徒のよさの発見,ねらいの達成) 興味関心を高められたか。数学的思考の重要性に気づいたか。 正弦曲線は印象に残ったか。身近な例に数学を意識することが出来たか。 |
| 【指導資料】 |
|
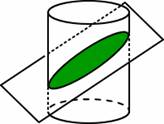
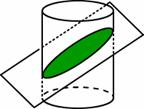
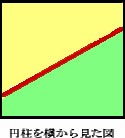
左図のように,半径1,高さ2の円柱と平面が交わっている。 平面と円柱の底面とのなす角は45°とする。
|
|
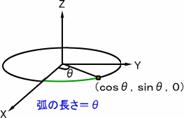
円柱の方程式は,X2+Y2=1 で表される。これを媒介変数表示すると, X=cosθ,Y=sinθ (0≦θ≦2π) となる。
このとき,左図のように,弧の長さはθに等しいという事実から求めることができる。 つまり,最初の立体図形で,切り口を平面上に展開した場合, 横軸がθ軸である。(円弧の長さを新たな物差しにするということ。)
ところで,平面の方程式は,X+Z=1としてよいので, Z=1-X=1-cosθ となる。
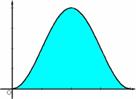
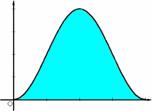
Z=1-cosθ (0≦θ≦2π) で,そのグラフは,左図のようになる。
左図の面積を求めると,高校生は積分を使うのが常識である。
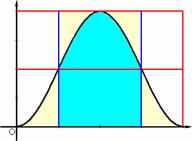
しかし,下記のように面積を暗算で求められる。
左図のように等積変形すると,求める面積は, 底辺の長さ= π 高 さ = 2 の長方形の面積となる。よって,答は,2πである。
また,円柱を横から見た図を考えれば, 平面が円柱の側面を真っ二つに切り分けていることがわかる。 側面積は,2π×2=4π なので, 求める面積は,その半分 2π と考えてもよい。
|
【その他アイデア】
|
鹿児島県立奄美高等学校 数学科 堂薗幸夫 http://www.synapse.ne.jp/dozono/ dozono@po.synapse.ne.jp |
|
SPP事業として今回の研修の目的は,数学的な知識を増やし,テクニックを身に着ける,ということだけに留まらず,「単に入試問題の解答に終始するのではなく,美しい数学を実験的に体験し, (1)他の分野と融合させる。(2)その背景に思いを馳せる。(3)深い理解につなげる。」ということではないかと考えている。そのため前述のような,三角比のグラフを実験して体験してみるという指導案を作成し提出した。更にその目的に照らして考え,資料検索し実践までは持ち込めなかったが,数点のアイデアを指導略案の形に仕上げたので,以下に列挙しておく。 〔資料サイト〕文部科学省 学習内容と日常生活との関連性の研究 http://www.mext.go.jp/a_menu/shotou/gakuryoku/siryo/05070801.htm 教育情報ナショナルセンター(NICER) http://www.nicer.go.jp/ |
(1)単元名: 数学Ⅰ 二次関数 二次関数とグラフ ~振り子のグラフ~
|
|
授業内容・活動 |
留意点 |
|
導 入
|
1583年のある日,ピサ大学の学生ガリレオは,ピサの寺院で,天井からつり下げられたランプの揺れを,自分の脈拍で測っていた。その揺れはだんだん小さくなっていくが,ひと揺れの時間は変わらないことに気づいた。 |
本時の実験にまつわる歴史上の逸話を紹介し,興味を持たせる。プリントを配り話す。振り子の法則性の存在を感じさせ,課題意識が持てるようにする。 |
|
展 開 1
|
3mの長さの糸と五円玉を数枚配り,振り子を作る。自由に振ってみる。2人ずつのペアで実験,計測をする。 10往復するのに何秒かかるか計ってみる。片道1秒の時計として使ってみる。周期はどうしたら変わるか考える。重りの重さ,振幅,糸の長さをそれぞれ変えて周期を計る。フリーソフト「質点単振り子シミュレーション」 |
重りの重さ,振幅,糸の長さ等を自由に変えながら周期を計る。その中から周期と糸の長さという2つの量の対応に着目するようにする。 振り子が1往復するのにかかる時間を周期ということを説明する。 |
|
展 開 2
|
身近な現象の中に数学があることを実感する。
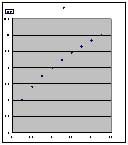
得られたデータをエクセルに入力し,グラフ化する。
具体的に操作することにより,法則が見えてくることを認識する。対応の関係を明らかにする手段として,グラフや数式など表現の工夫があることを理解する。糸の長さを0.25mから2.25mまで0.25mごとに変えて周期(10往復の平均)を計り,表にまとめる。 グラフはどのような曲線か考える。 式を立てることが出来るか。 |
表において,気づく点を出し合う。
放物線は中学の既習事項であるが,復習として説明する。
よりℓとTは2次関数になる。 |
|
展 開 3 |
式を利用すれば操作をしなくても予測ができることで,式で表現することのよさを感じる。周期が4秒になるのは糸の長さが何mのときか式により考える。 |
二次関数を数式の一般形で定義する。 二次関数グラフ=放物線を確認する。 |
|
ま と め |
解明したことを発展・利用していくためには統一した呼び方や記号,式による表現が必要かつ有用である。振り子実験は二次関数の一つの例であることを確認する。 |
自然現象を数学としてとらえていく視点や過程の中に,様々な見方や考え方があることを押さえる。 |
(2)単元名: 数学Ⅱ 音と三角関数と指数関数(等比数列) ~音で遊ぼう~
|
|
授業内容・活動 |
留意点 |
|
導入 |
本時の目標を説明する。音について,ギターとPCを使いながら数学的内容を掘り起こしてゆく。 電話のコール音はどうやって作られるか? |
多くの分野が含まれる内容のため,散漫にならぬよう手際よく進める。
|
|
展開 1
|
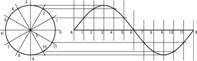
音が三角関数で学習した正弦波の形で表されることを説明する。フリーソフト「音オシロ」を使い,音叉の音を入力・表示させる。
フリーソフトGrapesを使って,時報の音などを聞き,実際に2つのサインカーブの和を表示させる。
振動数を大きくしていくほど音が高くなり,正弦波の周期も短くなることを,音とグラフから確認する。
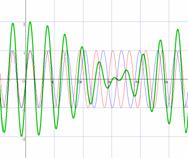
振動数がわずかに違う2つの音を別々に,次に同時に鳴らして「うなり」を起こして聞いてみる。 Grapesのスクリプトとして,下の音を左右のスピーカーから流す。 Play( t , 0 , 4 , (sin880Pit , sin888Pit)) フリーソフト「hatsune16.exe」も利用可能。
うなりが弦楽器の調弦に利用できることを例としてあげ,実際に演奏する。
倍の波長を聞かせて,次の実験につなげる。 |
聞きっぱなしにならないよう,プリントで2つのグラフの合成(足し算)を行ってみる。実際に2つの正弦波を足し合わせたものが画面のグラフ(プリントのグラフ)であることを説明する。
実際に聞く音の波形と,見やすいグラフとは違うため注意する。
音の「うなり」を知らない生徒もいるので,説明をしておく。
オクターブの意味を知らせる。 |
|
まとめ1 |
三角関数を使ってうなりのしくみを説明する。 角振動数ωを中心に前後に幅2αだけ角振動数がずれた2つの音を考えると,合成された音は次のようになる。
|
ギター内では,調弦のためにはうなりを必要とする。
実際に耳で聞き,サインカーブの和を感じる。
うなりでぴたり揃うが,音階は実はぴたりと揃っていないと次に繋げる。 |
|
展開2 |
次にギターを使い,音階について話を進める。 ある音と,オクターブ高い音の弦長を調べる。 ハーモニックスのでる5フレットや7フレットの弦長を調べる。単純な整数比となっている。うなりはなく,ぴたりときれいな和音を作る。(ピタゴラス音階・純正律)
フレット数を数える。12フレットで2倍の振動数になるということは,どのような数列で並んでいるのか考える。うなりが発生し,濁った和音を出す。(平均律)
ここに指数法則(等比数列)が成り立っており,2の12乗根の話題に触れる。 他楽器との音程を揃えるため,純正律ではなく,平均律であるということ。 フリーソフト「KSK Muscale.exe」を利用し実際に聞く。 |
フレット間の距離を測り,比を求める。
平均律での完全5度の振動数比は2の12乗根を7乗した1.49831~という値であるが,純正な完全5度では3/2 つまり1.5という比率になる。微妙な違いは,ウルフトーンと言われる。 |
|
まとめ2 |
純正律と平均律では,微妙な音程の違いがある。移調を正しく行うため,平均律が一般的に使われる。 音楽の中に様々な数学が含まれている。 |
シンセサイザーはその名のとおり「合成」して音色を作っている。
|
(3)単元名: 無理数の作図 ~ルートの根っこ~
|
|
授業内容・活動 |
留意点 |
|
導 入 |
無理数の発見をしたピタゴラスの歴史的背景について話す。我々が現在何気なく使う√は,歴史上大きな問題を持っていた。無理数の問題はギリシア人にとって算術の分野であるよりは幾何学のそれであった。最初に発見された無理数は正方形の対角線とその一辺との比すなわち√2であることは確かである。これはピタゴラス自身によるものではなく彼の学派において発見されたものである。しかし,この無理数の発見はピタゴラス学派に危機をもたらした。↗ |
↗というのは自然数とその比のみを算術の対象としていた彼らにとっては,√2:1が整数の比(有理数)として表わされないため,√2を数として認めるわけにはいかなかった。
歴史について触れ,口外してはならないものを口外して追放されたなどの逸話で興味を持たせる。プリント資料 |
|
展
開
|
√2は小数で表現すると,約○.○ぐらいか発問する。
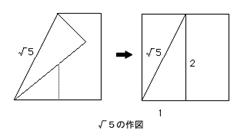
では,√2の長さをとるための作図法はどうすればよいか,発問する。
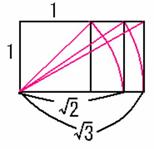
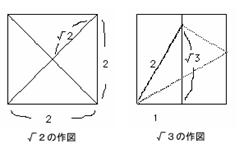
コンパスと定規で√2を作図する。 1:1:√2の直角二等辺三角形を作図する。 (1の長さの線分の先端に1の垂線を立てる。)
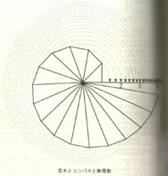
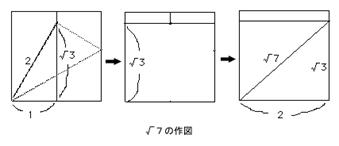
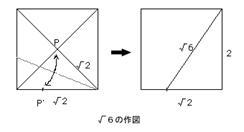
次に,√3はどうするか? 無理数を連続的に,数直線上にとってゆく。 12+(√2)2=(√3)2 12+(√3)2=(√4)2 と繰り返してゆく。
また,1辺2の長さの折り紙を5~6枚配布する。 折り方を工夫すると,√2~√8の値をとることが出来る。工夫して折ってみよ。
コピー用紙の縦:横の比率を計算させる。1:√2の白銀比と言われる。A4用紙とB4用紙との関係も調べる。(面積比が1:1.5やA4の対角線とB4の1辺の長さを互いに調べさせるなど。) |
覚え方,ひとよひとよに…を伝える。
三平方の定理について言及する。
√3をいきなり求めることは出来ないが,√2の長さを利用すれば出来る。 覚え方,ひとなみに…を伝える。
前の値を利用して,次の値を求める漸化関係になっている,つまり,コンピュータの得意な計算である。プラトンの著書「テアイテトス」によると,テオドロスが √3、√5、…… √17 までの数の不可約なことを証明したとある。
|
|
まとめ |
普通に使っている無理数にも,背景があり,少し工夫するだけで,簡単に得られることを押さえる。 |
無理数のだいたいの近似値を憶えることはおおまかな解のあたりをつけるために重要である。 |
(4)単元名: 二項展開 パスカルの三角形 ~隠された規則性~
|
|
授業内容・活動 |
留意点 |
|
導 入 |
(a+b)2=a2+2ab+b2は,おそらくクラス全員が覚えていると思うが,3乗の公式は?
ただし,例えば(a+b)3の項を書き出す際に,a2b2などありえない項を書く可能性もある。3次元の展開であるため,各項には必ず文字が3つずつ入るはずである。つまり,a3,a2b,ab2,b3の4種類しか存在しない。 |
基本事項の復習であり,規則性について類推させる。
次元についても触れる。 |
|
展
開
|
では,4乗,5乗の公式は? 係数だけに注目して,規則性を見つけ出して欲しい。
オセロゲームの駒のようなものを準備し,表と裏の出方を考えさせる。例えば,駒2枚の場合は,白白,白黒,黒白,黒黒といった,1:2:1の出方がある。 例えば,駒3枚の場合は,下図の通り。 ○○○ ○○● ○●● ●●● 1:3:3:1 ○●○ ●○● ●○○ ●●○
駒4枚,駒5枚を書き出し,確認する。 nCrを計算させ確認させる。
この数を偶奇で(奇数は黒,偶数は白)分類すると, シェルピンスキーのギャスケットといわれる自己相似図形が現れる。
また, のように傾き2の直線で,和をとると,フィボナッチ数列が現れる。
|
規則性を見つけ出すことが出来るか。 どんな項が出るはずか?どんな係数になると思われるか。
パスカルが,友人フェルマーと共同研究をしていたものがコレである。
一人当たりコイン2枚や3枚を投げさせ,クラス全体で出方の比率を求めさせても面白い。確率に発展してゆくことに言及する。
「人間は考える葦である。」彼は数学者であり,物学者であり,哲学者であり,文筆家でもある多才な人物である。
方眼の付いたプリントに書き出させ,マーカーなどで色を塗ってゆく。 フリーソフト「pascal」の利用。
フラクタルについての話題に入る。
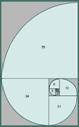
フィボナッチ数列についての解説も加える。 『1,1,2,3,5,8,13,21,34,55,…』
この数列は「フィボナッチ螺旋」と呼ばれる対数螺旋の形で, 自然界や生物に多く見られる。 |
|
まとめ |
単なる展開の公式から発展して,数字の列に,組合せや,確率,図形的にユニークな性質が潜んでいる。 |
オウムガイ,ミロのビーナスなどの画像の提示。 |
(5)単元名: 連続量と確率 積分での求積 三角形の成立条件 ~面積で確率を~
|
|
授業内容・活動 |
留意点 |
|
導 入 |
そうめんを一人数本ずつ配り,任意の位置で切断し,3つの線分を作る。 その3本の線分で三角形を作る。 どれくらいの人が出来たか。あるいは出来なかったか。 |
手軽な実験なので,数回試行させる。 ただし,人間の感覚では「三角形の出来上がってしまう切り方」を無意識のうちに行ってしまう。 |
|
展
開
|
人間の意識を混入させないため,乱数表を配布し,実験を再開する。 線分を0~10という仮の目盛りをとり,そのどの位置で切断するか,乱数表によって2点を選択させる。 その点で切断すると,三角形が出来るか?
三角形の成立条件とは何かを確認する。
自然数だけではなく,もっと切断の位置は自由である。 つまり,通常の教科書で行っているような,確率とは,(その条件を満たす試行の数)/(全体の試行数)という離散的なものだけでは通用しないことを認識させる。
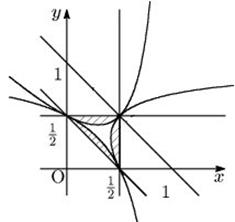
3辺の長さをどういった文字で扱うとよいか。 もとの線分を1として,x(>0),y(>0),1-x-y(>0) とおき,領域計算に持ち込む。 (1/8)/(1/2)=1/4である。
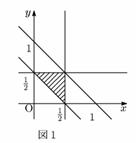
更に,そのうちで鋭角三角形になる確率を求める。
これは,2次曲線となり,下図のような積分を使った面積計算が必要になる。
更に,鋭角三角形となるか,鈍角三角形となるかどちらの確率が大きいかまで考えさせる。 |
乱数表をエクセルなどで作成しておく。乱数表とは,…という説明も加える。
この時点で,0や10や,同一の数を2点選択してしまったときに何が起こっているのか考えさせる。
連続量の確率計算は高校数学では登場しないが,十分理解可能である。
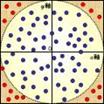
フリーソフトや,ネット上のJAVAプログラムなどで,モンテカルロ法の概略を提示する。
三角形の成立条件から,領域を示す。
鋭角三角形の成立条件から,同様に領域つまり面積の話になることに触れると,同様に立式を始める。
これが面積なので,三角形が出来たとき,それが鋭角三角形となる確率は,÷(1/8)して,12log2-8(≒0.318)が求める確率。
e>2.7を用いて評価することが出来る。 |
|
まとめ |
離散的なものに留まらず,連続的な確率へのアプローチと,立式,領域計算,図示,更には積分の面積計算へと多分野にわたってゆく面白さと意味を感じ取れたか。
|
|