 |
| 俀侽侽侽擭偺僙儞僞乕帋尡偱丆悢妛嘇偺悢妛嘦丒俛偵偍偄偰嶰師娭悢偺堏摦偵娭偡傞栤戣偑弌戣偝傟偨丅
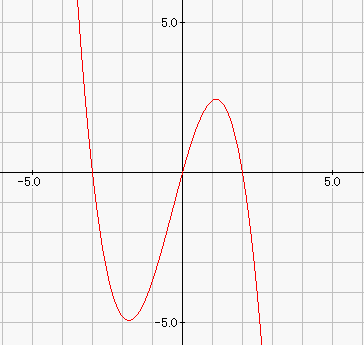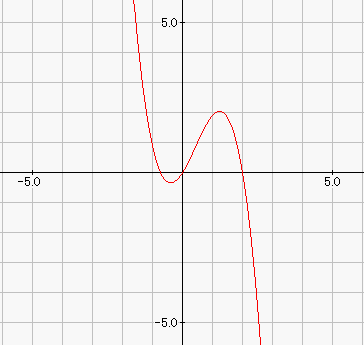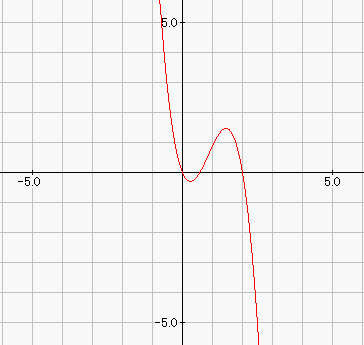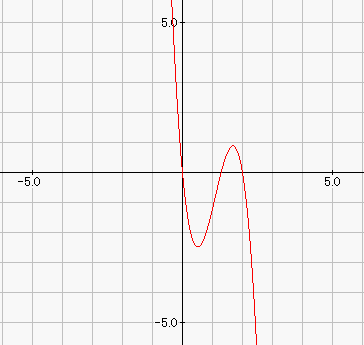
乮栤戣乯搑拞徣棯丒丒丒 丂丂乮俀乯倎傪侽偱側偄幚悢偲偡傞丅娭悢倖乮倶乯亖俁倎倶俀亅乮俉倎亄俇乯倶亄係倎亄俇 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倶 丂丂丂丂偑偁傝丆娭悢倛乮倶乯傪丆倛乮倶乯亖佺丂倖乮倲乯倓倲丂偲掕傔傞丅 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂0 丂丂丂丂偙偺偲偒倶亖侽偍傛傃倶亖俀偵偍偗傞倛乮倶乯偺抣偲旝暘學悢偼丆偦傟偧傟 丂丂丂丂倛乮侽乯亖仩丆丂丂丂丂丂倛乮俀乯亖仩 丂丂丂丂倛乫乮侽乯亖仩倎亄仩丆丂倛乫乮俀乯亖仩丂丂偱偁傞丅 丂丂丂丂侽亝倶亝俀偺斖埻偱倛乮倶乯偑惓偺抣傕晧偺抣傕椉曽庢傞偺偼丆 丂丂丂丂丂丂丂仩 丂丂丂丂倎亙----丂丂偺偲偒偱偁傞丅 丂丂丂丂丂丂丂仩 偙傟偑乮侾乯偼徣棯偟偨偑丆乮俀乯偺栤戣偱偁傞丅丂 峏偵夝摎傕堦晹徣棯偡傞偑丆 丂丂丂愊暘偡傞偲丆倛乮倶乯亖倎倶俁亅乮係倎亄俁乯倶俀亄乮係倎亄俇乯倶丂偲側傞丅 丂丂丂偙傟偵戙擖偟偰丆倛乮侽乯亖侽偱偁傝丆倛乮俀乯亖侽偱偁傞丅 丂丂丂傑偨丆旝暘偡傞偲倛乫乮倶乯亖俁倎倶俀亅俀乮係倎亄俁乯倶亄係倎亄俇偱偁傝丆 丂丂丂偙傟偵戙擖偟偰丆倛乫乮侽乯亖係倎亄俇丆倛乫乮俀乯亖亅俇偱偁傞丅 慜抲偒偑挿偐偭偨偑丆傗偭偲愒偺晹暘偺夝愢偲恾宍揑堄枴偱偁傞丅
乮夝愢乯 旕忢偵桿摫偑恊愗偱偁傞丅 扨偵丆侽亝倶亝俀偺斖埻偱丆惓傕晧傕丒丒丒偲偩偗弌戣偟偨側傜丆 掕揰乮侽丆侽乯偲乮俀丆侽乯偼尒偮偗弌偣偢偵丆惓摎棪偼掅偐偭偨偱偁傠偆丅 乽擇師娭悢偺堏摦偵傛傞捀揰偺嶌傞婳愓乿側偳偼丆掕斣偲偟偰偺弌戣偱偁偭偨偑丆 偮偄偵乽嶰師娭悢偺堏摦偵傛傞忦審偺専嶕乿偺悽奅傑偱撍擖偟偨丅 偄偔傜桿摫偑偁傞偲偼偄偊丆寁嶼偩偗偵偼棅傟側偄丆僀儊乕僕偑昁梫側椙栤偱偁偭偨丅 偟偐偟丆椺擭偺栤戣側傜丆弴彉偼旝暘偟偰偐傜愊暘乮偦傟傕柺愊乯偩偭偨偑丆 愊暘偑愭偩偭偨傝丆柺愊傪栤傢側偐偭偨傝丆栄怓偺曄偭偨栤戣偲尵傢偞傞傪摼側偄丅 |