(解)
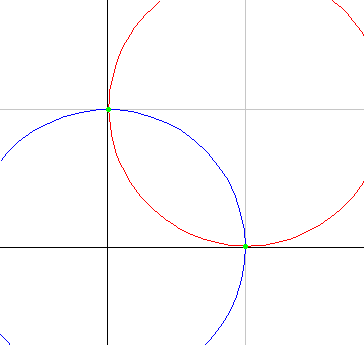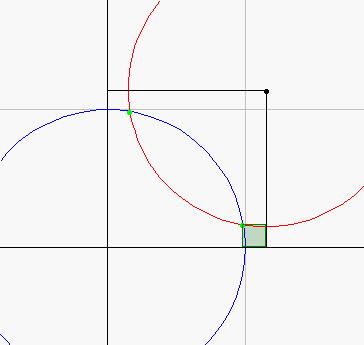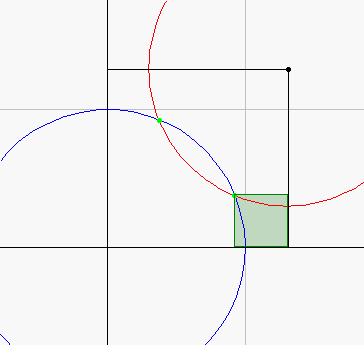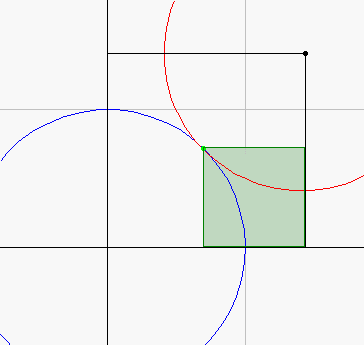
(1) w=γ+zだから,wはzをγだけ平行移動したものである。よって上図のとおり,wは点γを中心とした半径1の円周上を動く。
(2) w=γ+z
√5 √5
=(---+---i)+(cosθ+isinθ)
2 2
√5
√5
=(---+cosθ)+(---+sinθ)i
2 2
|w|=1より|w|2=1だから,
√5
√5
(---+cosθ)2+(---+sinθ)2=1
2
2
5
5
---+√5cosθ+cos2θ+---+√5sinθ+sin2θ=1
4
4
√5
sinθ+cosθ=- ----
2
また,
√5
√5
w=(---+cosθ)+(---+sinθ)i
2 2
=a+bi だから,
√5
√5
√5 √5
a+b= ---+cosθ+---+sinθ=√5-
--- = ---
2
2
2 2
(3) 交点の座標を,α=a+biとおく。 αは,C1上にあるから,a2+b2=1 また,αはC2上にもあるから,
√5
a+b=--- である。
2
この2式を連立すると,
√5+√3 √5-√3
a=---------- , b=-----------
4 4
および,
√5-√3 √5+√3
a=---------- , b=-----------
4
4
となり,それぞれに対応する2つの交点α=a+biが求まる。
【解説】
出題されたてのホヤホヤ(2000,2/25実施 2000,2/26作成)の問題。わが母校の鹿大ゆえ,毎年気になるところです。
複素数平面上の図形の問題とは言え,内容は実質的には,数学Ⅱの「図形と方程式」の円の問題と読みかえる事が可能である。
とはいえ,複素数での図形の表現は相変わらず,わかりにくいですねェ。円の定義のように,「ある点から等距離にある点の集合」という意味や,ベクトル的な発想,もちろん基本的な計算も,多くの知識を必要としますよねぇ。
移動中の円は問題ではなく,移動後の円と元の円との関係を問うているので,上図のようなアニメは本来は必要はなかろう。が,問題の言ってることは,上図のとおり,たったこれだけなのである!
問題を発展させて,一般的に次のようなrが言える。
複素数zと,複素数wの間に,w=γ+zの関係がある。
ただし,γ= r(1+i) とする。
C1は原点を中心とする半径1の円とする。
C1上の点zに対応する点wが|w|=1のとき,
w=a+biとすると,a+b= r となる。
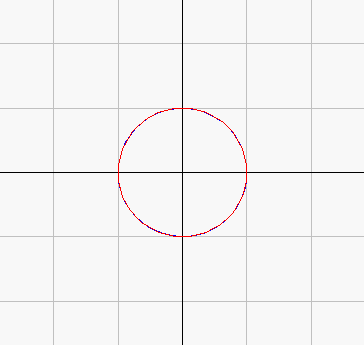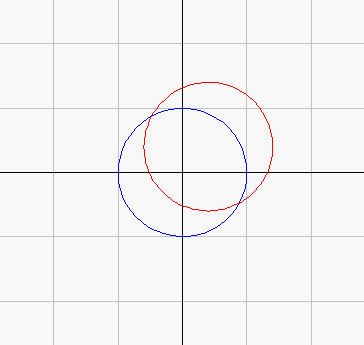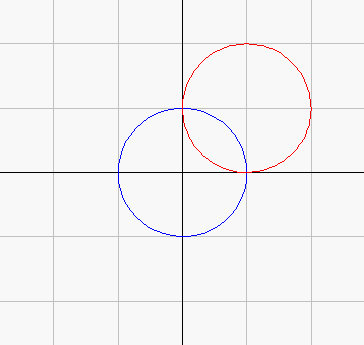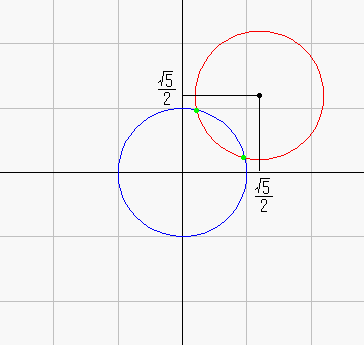
これを表したのが,右の図である。
薄い緑の四角形は正方形である。
このとき,二円の交点が第一象限において存在するためには,
1<r≦√2でなければならない。
(交点の数は,r=√2のとき1個。他は2個。)
(C2の中心のx(or y)座標)は,(交点のx座標+y座標)である。 |
 |
|