|
本日行われた,今年のセンター試験。あったかいうちにやっつけちゃおうと,終了後数時間でのレポートです。
大き目サイズの問題は,こちらからどうぞ。
この中の(3)を動かしてみた。
|
||||||
|
(解説)
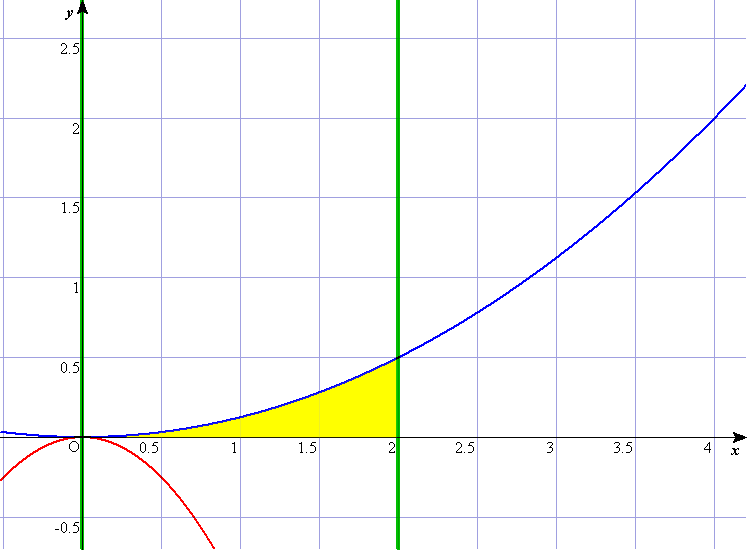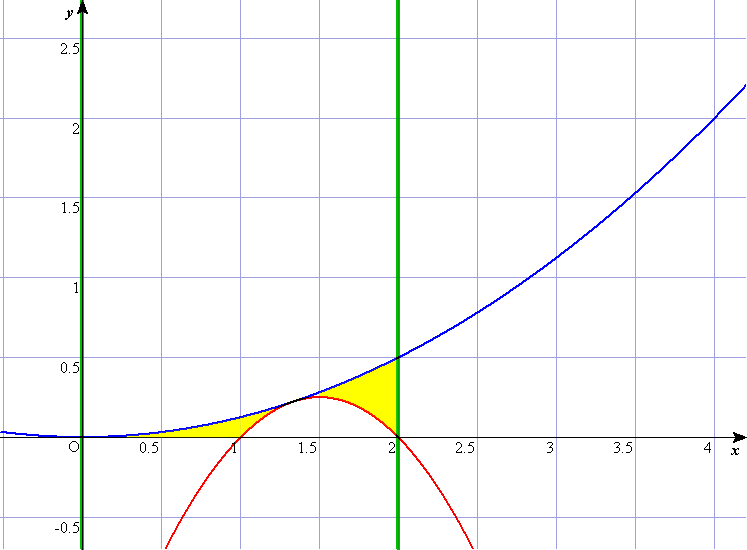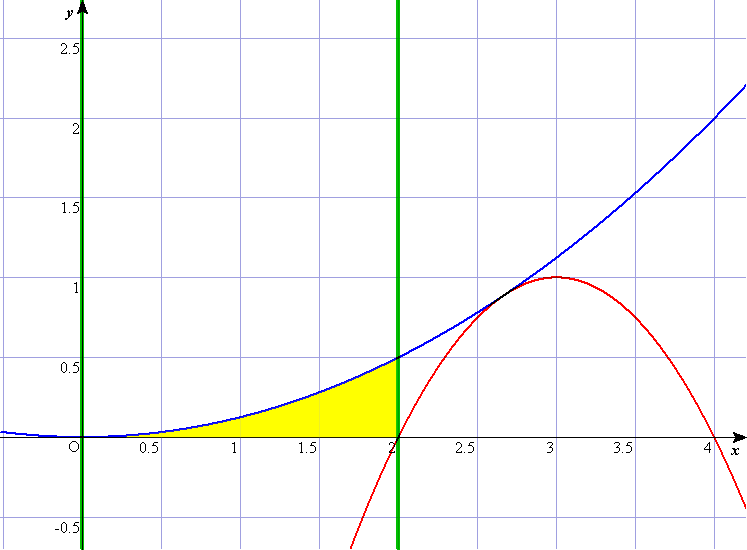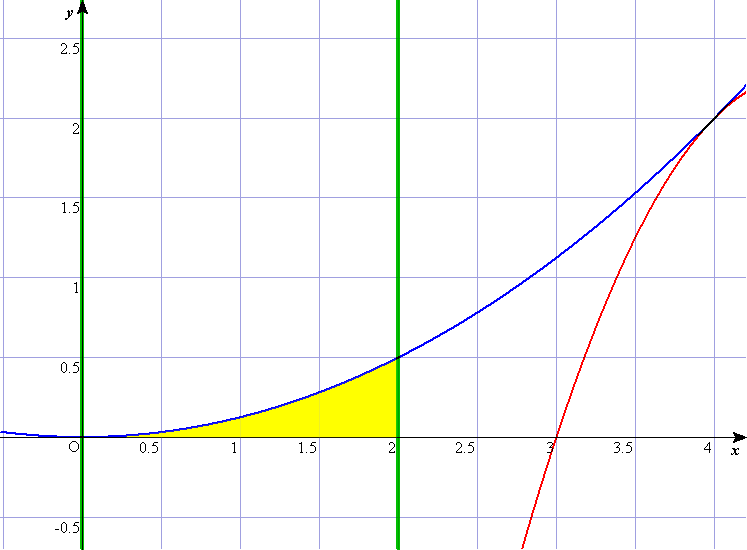
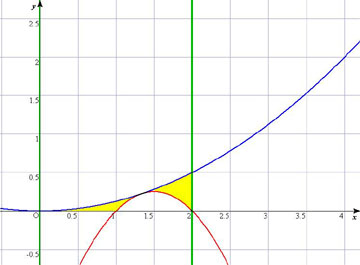
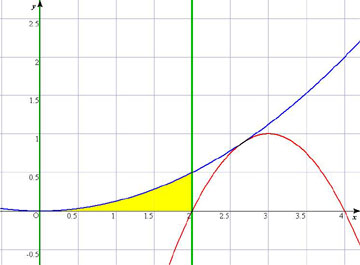
C2のグラフは,上に凸の赤のグラフであり,(2)よりx軸とはx=a,2aとで交わっている。 ご覧のように, (i) aが0〜1の範囲と, (ii) 1〜2の範囲と, (iii) 2〜 の範囲 これが,(3)の問うていることである。 誘導として,(2)においてC1(これは,青のグラフ)とx軸とx=2(これは右側の緑の直線)に囲まれた部分の面積として,ケコで1/3を計算させている。これが(iii)の誘導となっている。薄い□をヒントに活用しなけらばならない。 **************************************************************************** ⅡBの計算量の多さに,辟易しながら,今年は微分積分の問題に動く図形イメージがあった。 でも,それを解きながら,いつものように,「分数計算めんどくさいなぁ・・・,計算ドリルをもっとやっとかんといかんなぁ・・・,100ます計算って重要なんだねぇ・・・,センター試験って発想力や着眼力よりも,計算力を重視してんのかなぁ・・・」なんてことをとつぶやいていたのだった。 さて,ぶつぶつ言うのはここまでで,モンダイの裏側を推測して解説。 ・2次関数の二つのグラフを絡めて,ひとつは固定,ひとつは接しながらずれて動く。そこに共有点や接線や面積を絡めてきたという出題である。ま,ありがちなテーマである。 ・しかし,微妙な動き具合(とーっても狭いところに重要なポイントがある)ことと,薄いほうの□がヒントになるという,センター特有のモンダイが前後してしまって,モンダイが発生しそうな,出題であった。 ・前述の接線だが,とりあえず微分も出題しとこっと。って感じで後の問題とは何ら関係なく,残念。 ・囲まれた図形をRとしながら,更にその中で,y≧0を満たす部分,という2段構えにしている。これは,いっぺんに表現して,〜かつ〜である,というややこしそうな表現を避けたのだろうと思われるが,いかがだろうか。
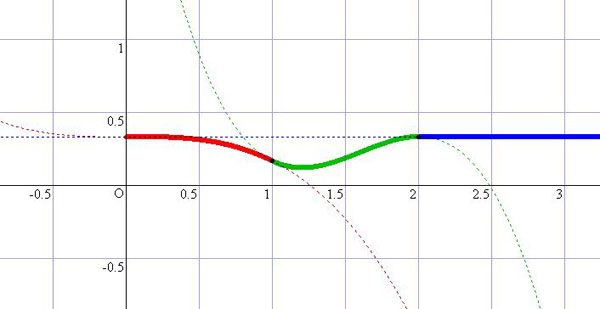
最後に,S(a)の変化を,グラフにしてみた。縦軸がS,横軸がaである。 太線部の赤が(i),緑が(ii),青が(iii)の三パターンの場合わけである。 今回は,GRAPESを利用してグラフ作成をし,photoshopで加工し,Giamでアニメーション作成を行った。 GRAPESのファイルもアップしてあるので,お暇な方はこちらから,gpsファイルをどうぞダウンロードください。 |