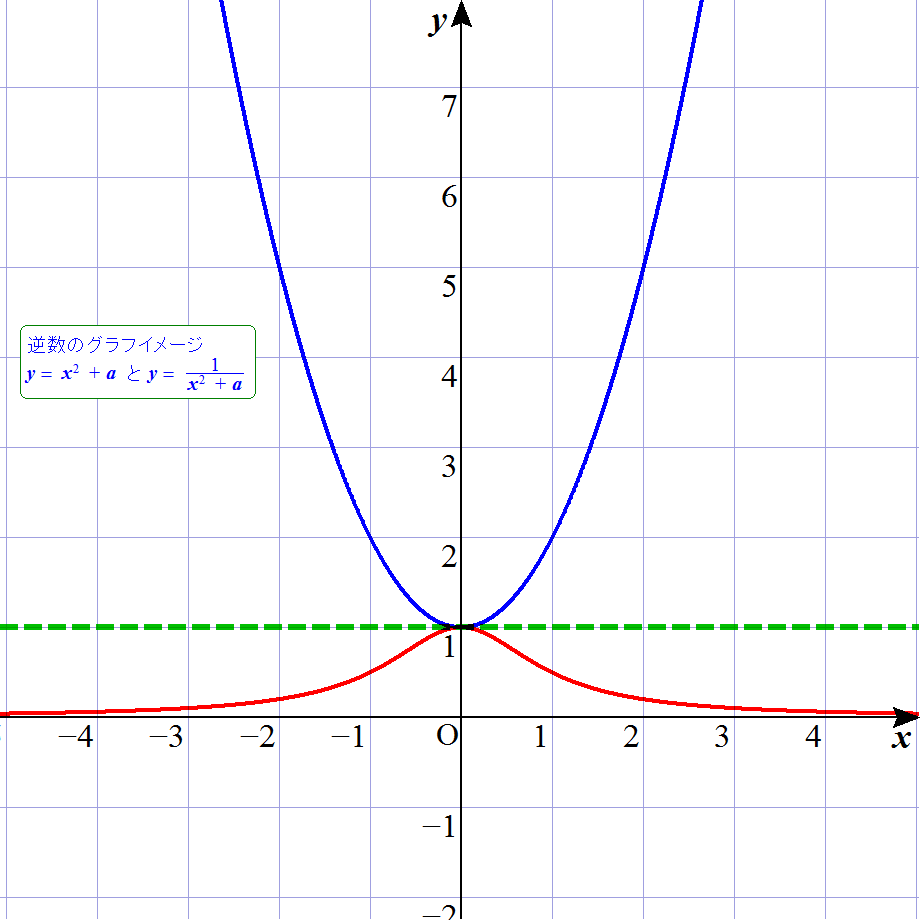
下の二つの赤と青のグラフを比較してほしい。
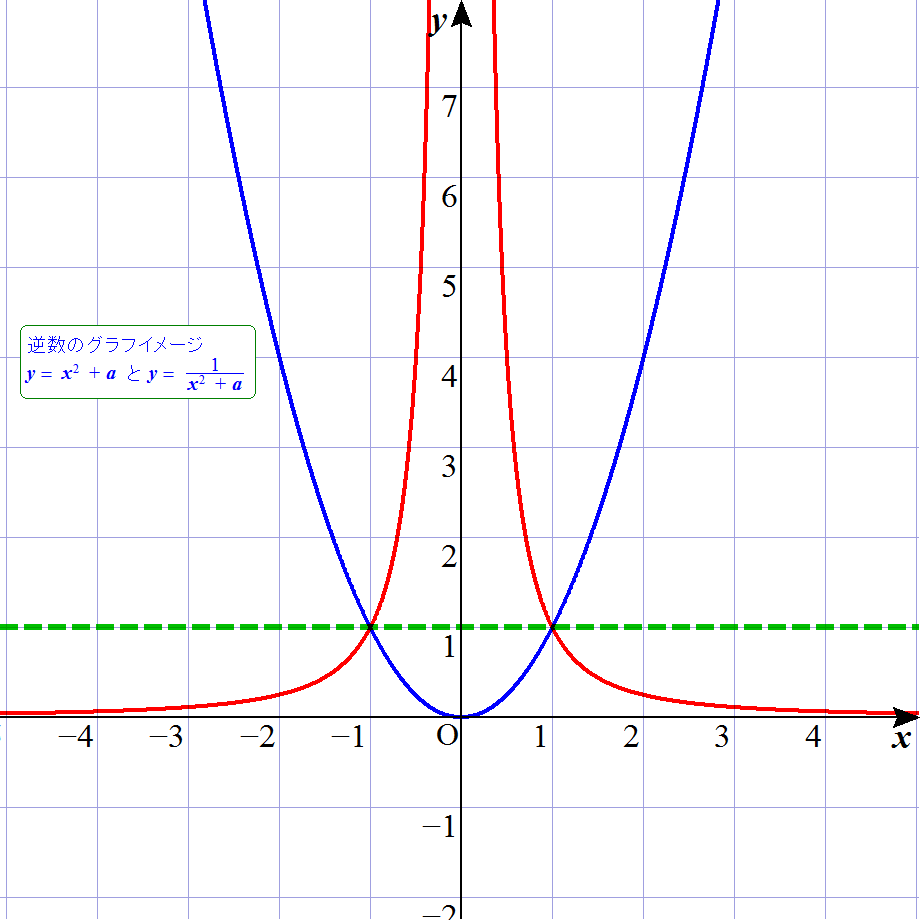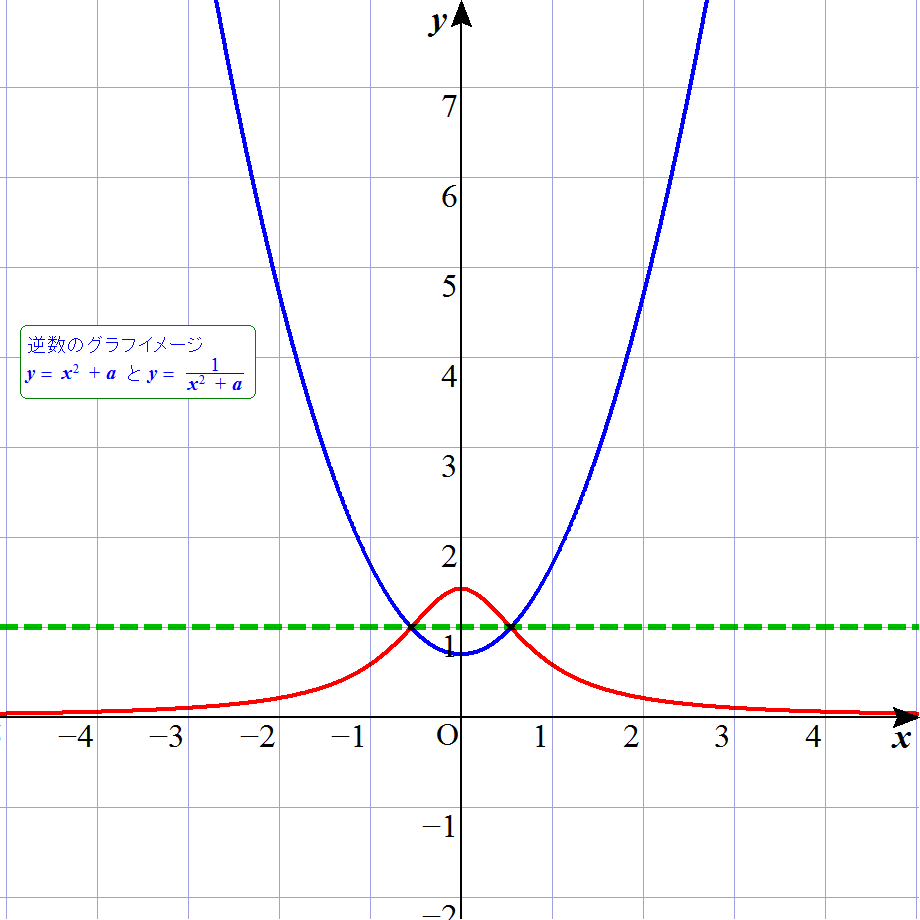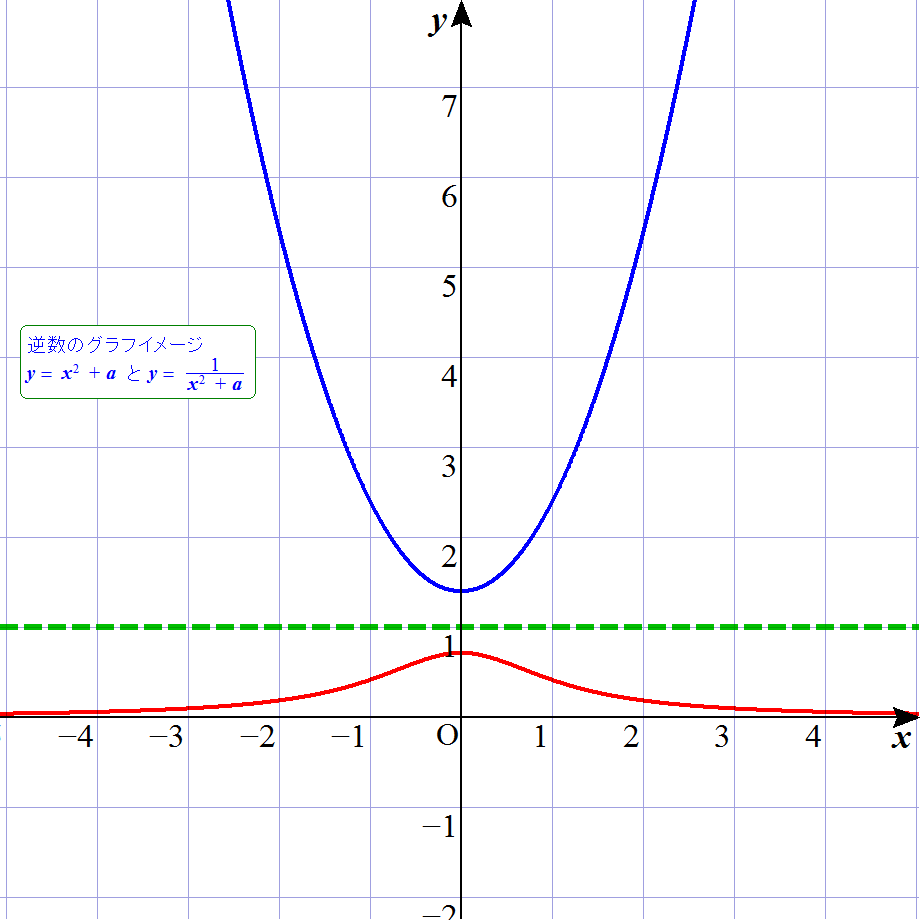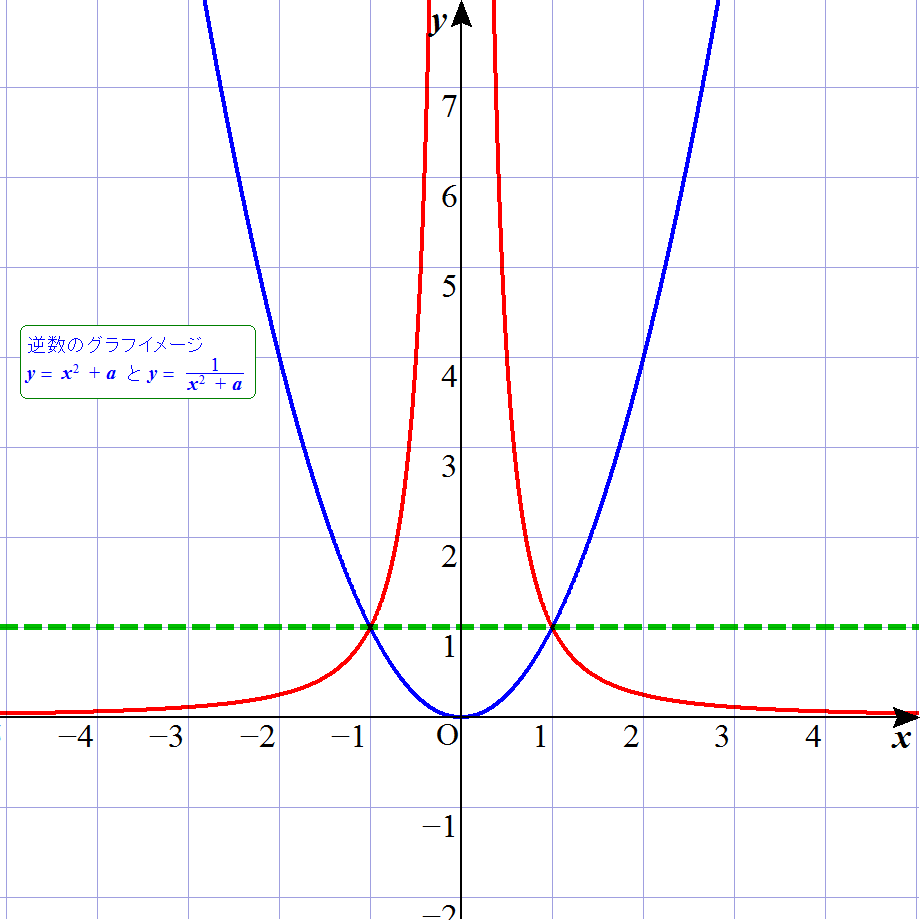
青のグラフは,中学校3年生で学習する2次関数で,y=x2+1 の状態である。 それに対して,赤のグラフは,正式には高校3年生辺りの数学Ⅲで登場する分数関数のグラフであり,y=1/(x2+1) を描いている。 で, 何が言いたいかというと,こんなに学習時期が3年間も離れているのだが,逆数的発想だったら同時にできるでしょ? ってことである。 以下のアニメを見て欲しい。
これは,先ほどのグラフが,a=1の瞬間のことであり,一般的に,y=x2+a と,y=1/(x2+a) を描き,aを変化させている。 逆数とは,y=1(グラフ内の緑点線)に対して,上下反転するイメージである。 もう少し具体的に言うと,x=3においてのポイントを見るなら,32=9なのか,1/32=1/9 なのかの違いである。 これが,例えば,x=1/3においては,更にその逆と考えられ,1/9なのか,9なのかである。 つまり,∞においては,1/∞=0を意味し,0においては,1/0=∞を意味しているのである。(分かる??) ところで,私は,赤グラフの方を富士山状のグラフと称している。
|
|||||
|
まとめ 結局何だったかというと,長くなったが,逆数というものはイメージできるということです。 上下反対,とか 大きいほうが小さい,とか,小さい方が大きいとか, こんなことを想像できるってのが,数学の面白さでしょうね~~。自由ですね~。
参考資料は,こちらから。2012.8の郷中ゼミ資料 |