|
先日,(と言っても2014年の夏休み8月,もう2か月も前だ!),郷中ゼミの授業を見学した。
私も数年前に,担当した講座で,その講座って?という方は,こちらからリンクをご覧ください。
積分計算に手間のかかる,しかし大切な概念を内包する問題であったので,勢いでアニメを作成した。
(問題)

3 次の条件(i),(ii),(iii)をみたす関数 f(x) (x>0)を考える。
(i) f(1)=0
(ii) 導関数 f'(x) が存在し,f'(x)>0
(iii) 第2次導関数 f''(x) が存在し,f''(x)<0
(1) a≧3/2 のとき,つぎの 3 数の大小を比較せよ。
f(a) , (1/2){f(a-1/2)+f(a+1/2)} , ∫(f(x)dx,a-1/2,a+1/2)
(2) 整数 n(n≧2)に対して,次の不等式が成立することを示せ。
∫(f(x)dx<Σ(f(k),k=1,n-1)+(1/2)f(n),3/2,n)<∫(f(x)dx,1,n)
(3) 次の極限値を求めよ。ただし,log(,?)は自然対数を表す。
lim((n+log(n!)-log(n^n))/log(n),n,("∞"))
(解説)

【考え方】
微分積分の総合的な知識が必要な難問である。問題から発せられるメッセージは,(1)では,グラフを想像できるか。平均という感覚があるか。面積はどうなっているか。といったところだろう。(2)では,面積評価が,Σ と関連付けられて繋がっていくことを想像してほしい。(3)は,log(,?)という具体的な関数が与えられているので,何を言わんとするか解り難い極限ではあるが,(2)ができていれば,はさみうちの原理で評価できる可能性が高いだろう。書き始める前に,想像力を豊かに方針をじっくり練って,「問題のもつ気配」を感じ取ることが大切である。
(略解)

【略解】
(1) y=f(x) は,(i)(ii)(iii)の条件から,x>0 において単調増加の上に凸なグラフをえがく。
x=a における,y=f(x) の接線をひき,そこにできる形状で面積を評価すると,
(内接台形)<(定積分)<(外接台形) が成り立つので,(x 軸方向の幅は 1 であることに注意)
計算して,(1/2){f(a-1/2)+f(a+1/2)} < ∫(f(x)dx,a-1/2,a+1/2) < f(a) が成り立つ。
(2) a-1/2 と a+1/2 の幅は,1 である。この 1 の幅を持つ台形をぴったりと隙間なく正の方向へくっつけていくと,
(1)で得られた不等式が,x=1 から x=n までの範囲での面積評価に繋がる。( f(1)=0 も効いてくる。)
ぴったりと隙間なくくっつけたので,Σの形に表現できるわけである。
つまり,(1)の結果を,A<B<C とし,(2)の示したい不等式を,X<Y<Z とするならば,
(1)の A<B の部分が,(2)の Y<Z の部分に,そして,(1)の B<C の部分が,(2)の X<Y の部分になる。
ただし,後半の X に相当する ∫(3/2) の3/2 の評価には,ひと手間かかるため注意が必要である。
(3) (2)が出来てさえいれば,簡単である。((1)(2)が未解答でも,(2)の結果を利用して(3)を解いて,部分点はもらえると
思われる。合格している人はその程度の受験テクニックは身に着けているはずである。白紙だと 0 点に違いない!)
f(x)=log(x) が条件をみたすことをいい,(2)の X 部とZ 部について計算を進めると,X と Z の極限は一致する。
つまり,はさみうちの原理から,Y 部が(3)の示したい極限値になっているわけである。
∫(log(x)dx)=xlog(x)-x+C を想像し,定積分で x=n とするならば,nlog(n)=log(n^n) が生まれて,
Σ はlog(1)+log(2)+…+log(n)=log(n!) へと変化していくわけである。
資料と考え方と,長かった。
具体的なイメージ図としては,
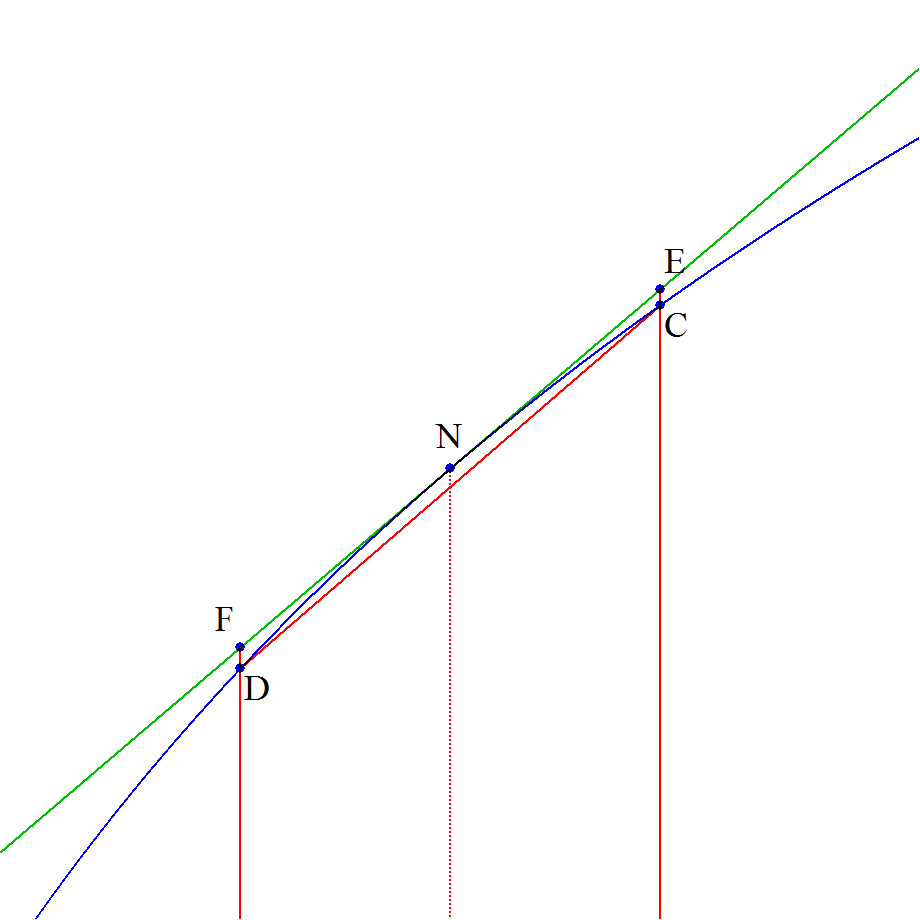
のように,上に凸な関数の接線と平均変化率などが想像できればいいのでしょう。これは,イェンゼンの不等式(いぇんぜんのふとうしき、英語: Jensen's inequality 凸関数を使った不等式)が元ネタであると考えることが出来る。
やっと来た。面積評価のアニメを作りました。
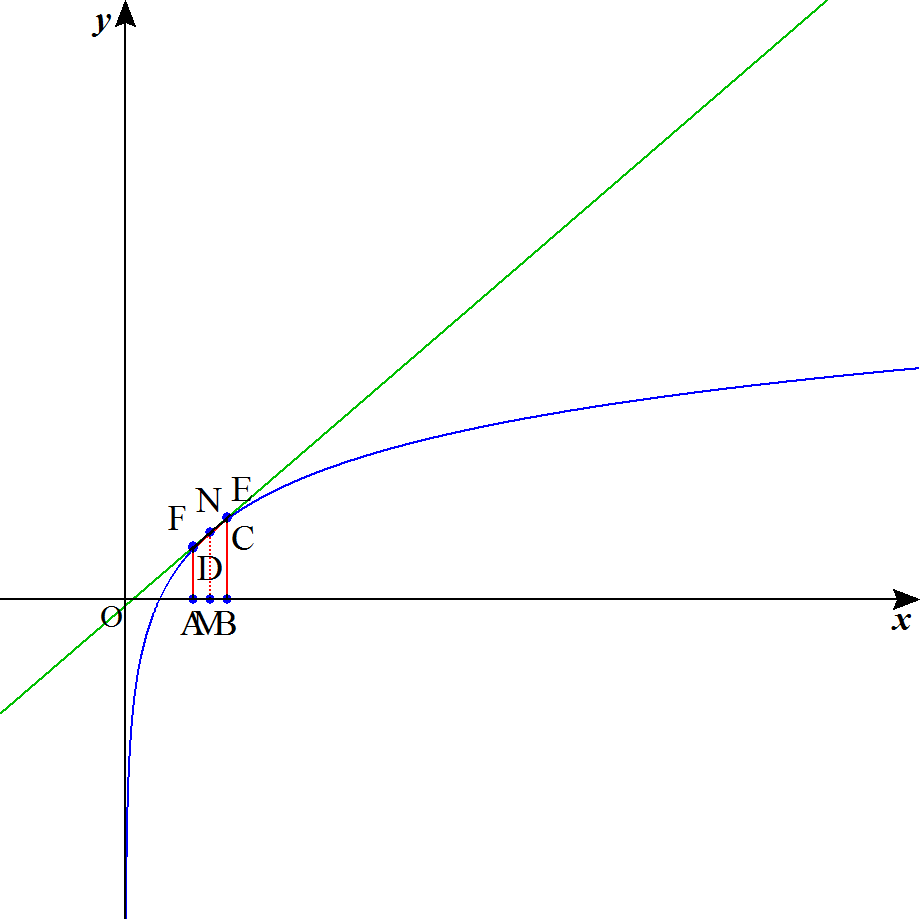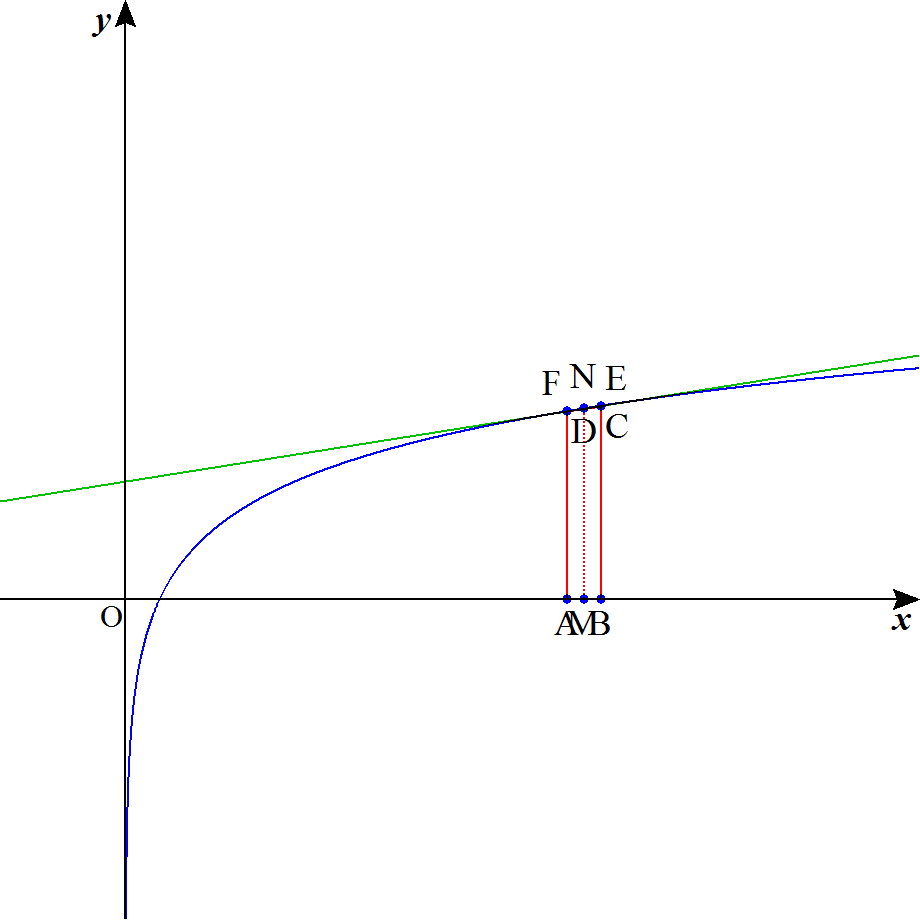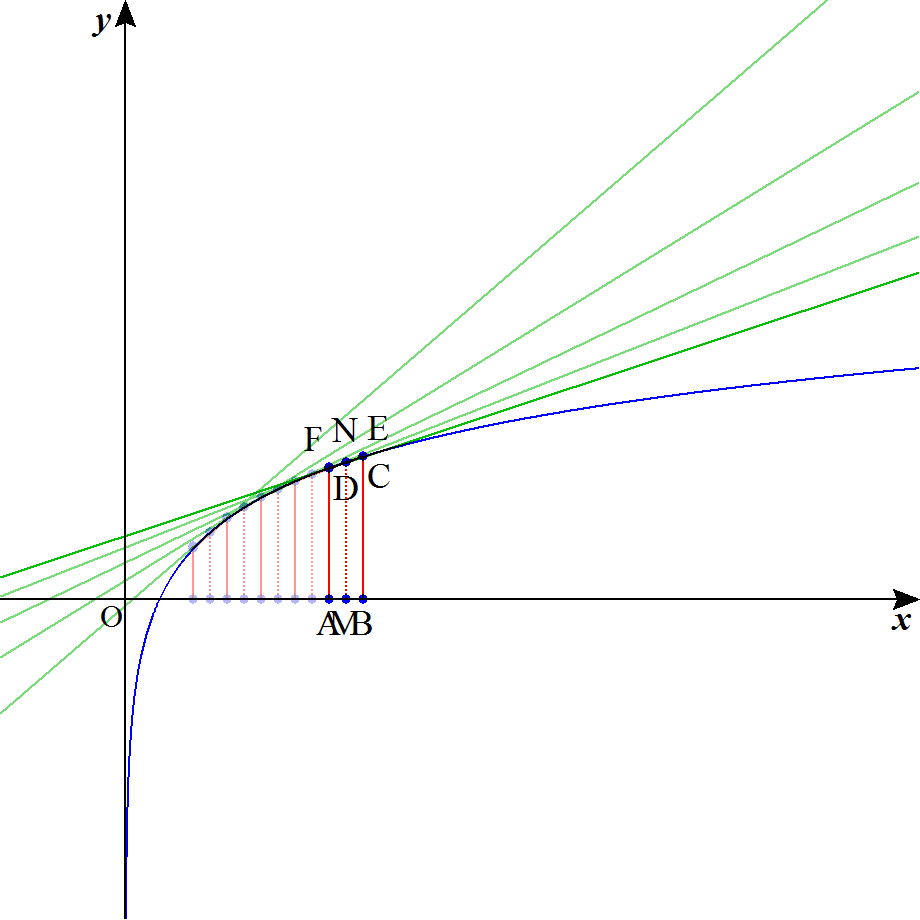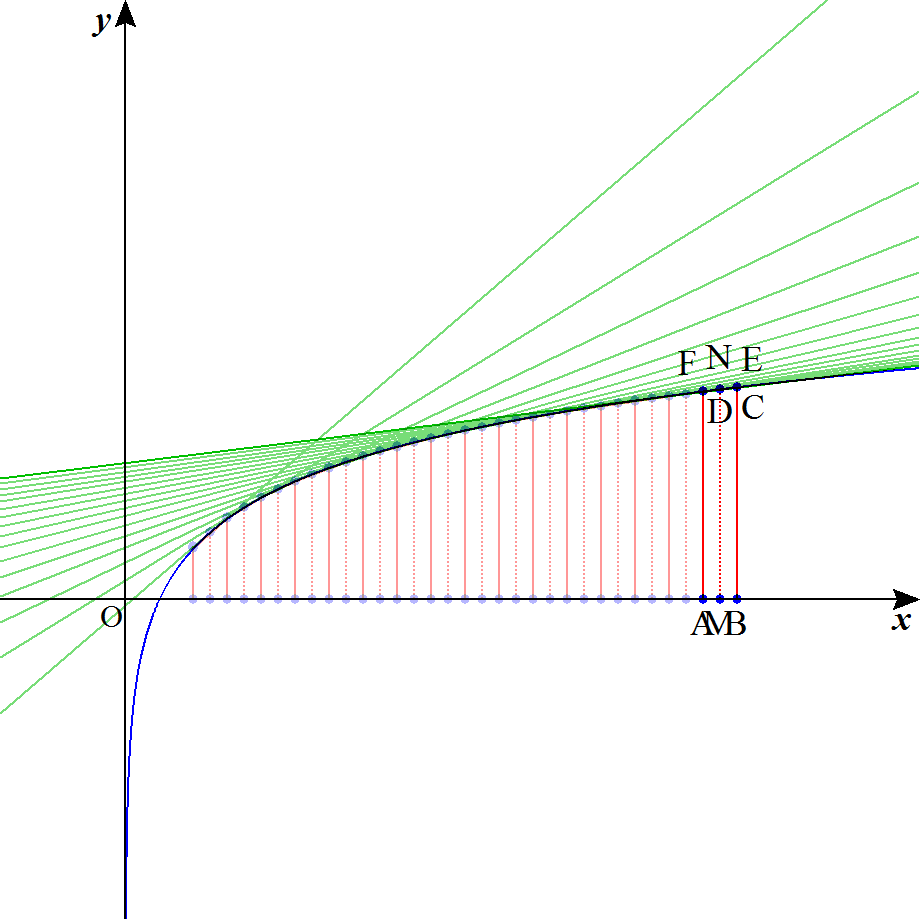
(ちゃんとした資料はこちら)
PDFの原稿は,こちらから ikashika2005-pdf.pdf
Grapesのアニメ作成データは,こちらから ikashika2005-sekibun.gps
(エピローグ)
授業を見ていると,ぼんやりとグラフが見えてくるときがある。
頭の中で,数式が変換され,動いている図が見えたとき,なーるほど!これが言いたかったのか!という瞬間がある。
そんな感覚が,もし,毎時間得られたなら,数学は「数楽」に変わり,ドーパミンが溢れ出すのかもしれない。
なかなかそんな感覚を得ることが難しく,やはり,数学は「数が苦」のままなのかも・・・?
楽しいよ,考えてみよう!
数学に挑もうぜ〜〜!
(メモ)
2014.8月の郷中ゼミ 問題3から
Grapesでデータ作成
Studiaidでプリント作成
FastStoneCaptureで画像キャプチャー
|




