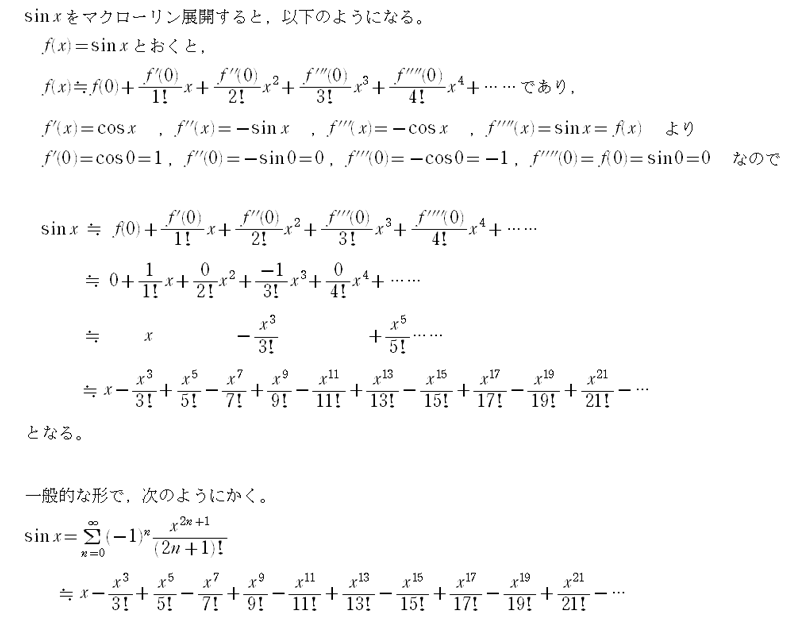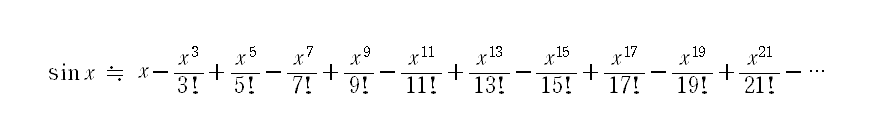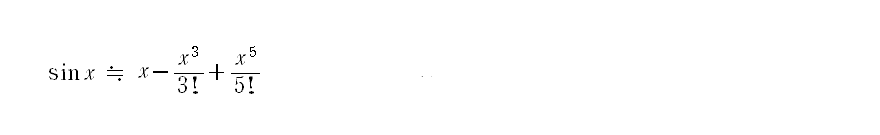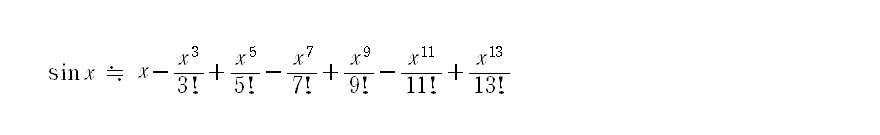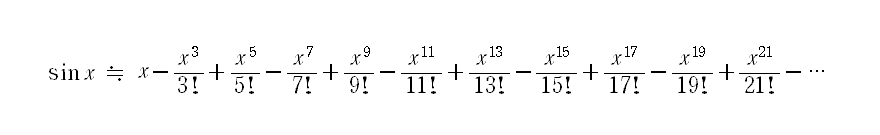テイラー展開とマクローリン展開

（テイラー展開とマクローリン展開）　Taylor expansion　＆　Maclaurin's expansion　　2008.1.30

サインカーブをマクローリン展開で近似したグラフを次々かくと，，，，

っとなるお話。

テイラー展開，マクローリン展開というものがあるが，高校数学では「ちら」っと触れるだけで，
そこまで入り込む時間も，余裕も無いのが現実である。
更に言うと，「ちら」見が出来るのは，それなりの学力の高い学校で
それなりの理解力を持った生徒でなければ，かえって微積分の混乱を深めるだけかもしれない。
興味と関心と，ちょっとした勇気と大胆な発想と，繊細な集中力があれば，
テイラーさんもマクローリンさんも，そう難しい事ではない。

さて，前置きはこの程度で。

【問題】

ｙ＝sinｘにおいて，次のｘの値のときに，ｙの値を求めよ。
(1)　ｘ＝π　　(2)　ｘ＝π／２　　(3)　ｘ＝１

【解答】

ラジアン表示されたｘにおいて，sin（正弦）の値を求めよという問題なわけである。
ちなみにラジアン表示とは，３６０°＝２π，１８０°＝πの形で角度を表記したものである。
つまり(2)のπ／２は，９０°ということになる。
(1)　ｙ＝sin１８０°＝０　である。
(2)　ｙ＝sin９０°＝１　である。ここまで簡単。
では，(3)　ｙ＝sin１　？？

１はラジアン表記された角度なので，表現方法を□°の形に変形すると，
１８０°：π＝□：１となるので，
□＝１８０°÷π＝１８０°÷３．１４１５９２・・・＝約 57.295…°となり，
ｙ＝sin１
　＝sin57.295…°
　＝？？？となって三角比の表が必要になりますね・・・。

妙な感じするでしょ？

でも値はちゃんとあるわけですよ。
これって，どーやって計算したのか？っちゅーところが問題のモンダイなのです。

ちなみに表によると，
　sin57°＝0.8386705679454239
　sin58°＝0.848048096156426
のようです。

しかし，次の計算をすると，近い値が出るのですよ。
ｙ＝sin１
　　　　   １^３　     １^５　   １^７
　＝１－----＋----－----
　　　　　３！　　５！　７！
　＝0.841468254　（エクセルで計算）
近そうでしょ？sin57.295…°って言われても，どーしようも無かったわけですが，
この計算だったら，手と紙と鉛筆と出来れば電卓を持っていれば，根性で出ちゃうわけです。

逆に言うと，πについても，近似値π＝3.14とするならば，
ｙ＝sinπ
　＝sin3.14
　　　　　   3.14^３     3.14^５　　3.14^７
　＝3.14－-----＋-----－-----　
　　　　　     ３！　     ５！　   ７！
　＝-0.073292015　（エクセルで計算）

となって，ほぼ０に近いですよね。
手で計算できるところが，テイラー展開，マクローリン展開の良さなのです。
この，マシンではなく「手で」というところが肝心ね。

さて，そのグラフを書いてみると一目瞭然。
あら不思議，ｙ＝sinｘのグラフと，それをテイラー展開したグラフは，
かなり一致しますね。精度を上げていけば，より正確になるわけです。

　　　　　さて，上の「妙な＋－の式」の数学的解説です。

微分可能な曲線y=f(x)上の点，(a,f(a)）における接線の方程式は，
x=aにおける微分係数，ｆ'(a)を利用して，
y-f(a)=ｆ'(a)(x-a)より
y=f(a)+ｆ'(a)(x-a)とかける。

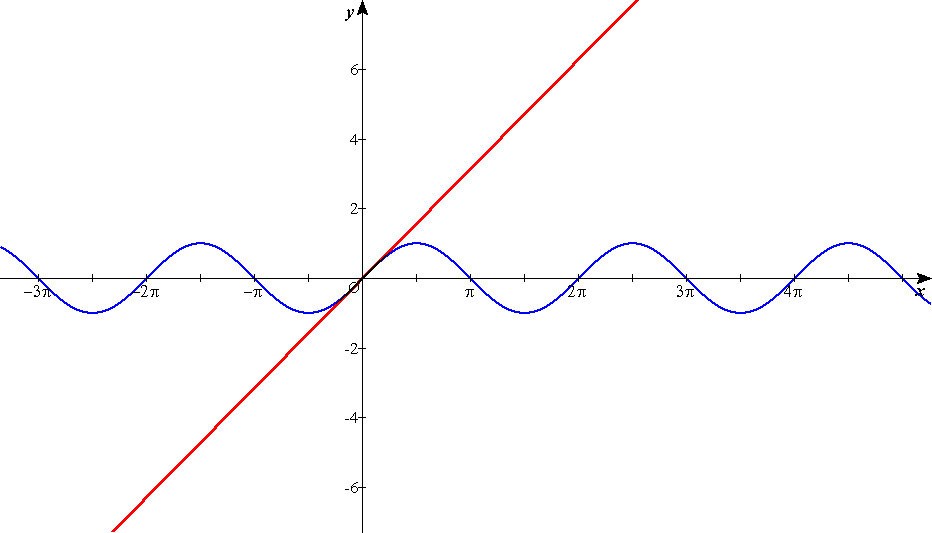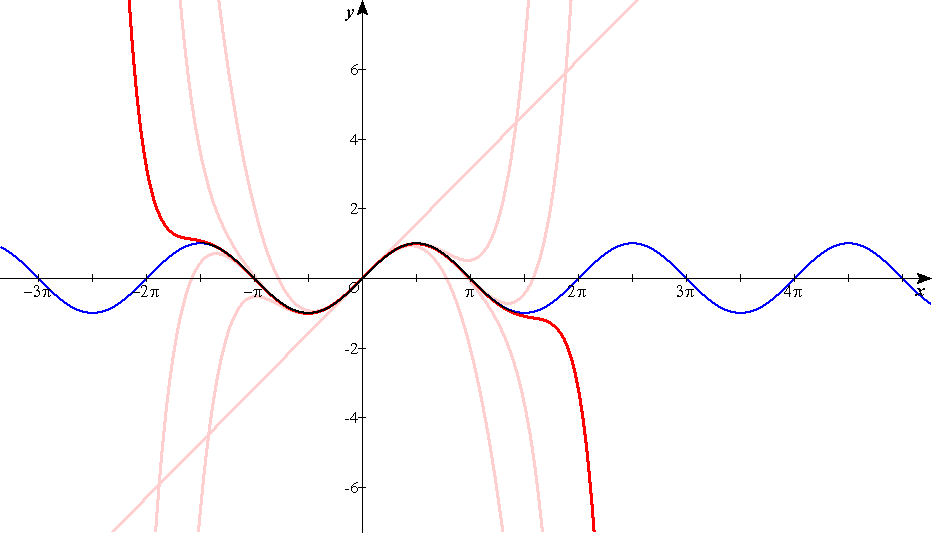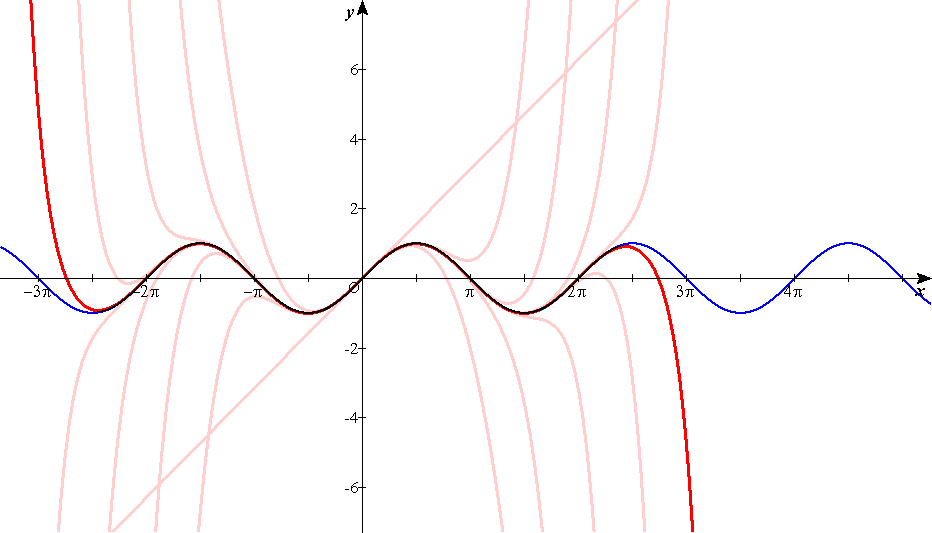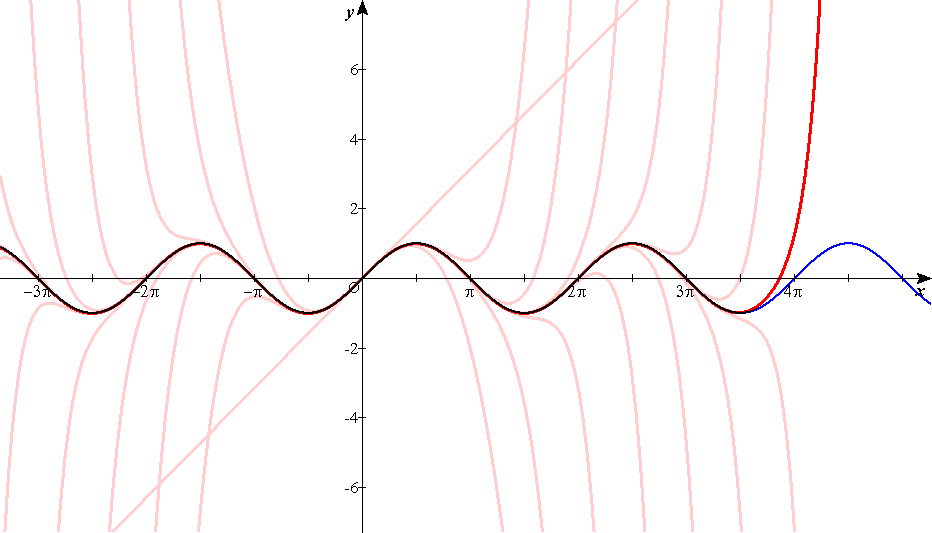
これは，x=aの近傍で，もとの式y=f(x)と非常に近いことが言える。
つまりこれを一次近似と言い，
f(x)≒f(a)+ｆ'(a)(x-a) を意味する。（一次式で近似したという。）

======================================================

この精度を上げて，二次式で近似しようとすると
f(x)≒f(a)+ｆ'(a)(x-a)+p(x-a)²…①

となる。

このpを求めると，
①の左辺を微分して，
　(左辺)=ｆ'(x)   x=aとすると (左辺)=ｆ'(a)
①の右辺を微分して，
　(右辺)=ｆ'(a)+2p(x-a)   x=aとすると   (右辺)=ｆ'(a)
(左辺)=(右辺)となり，成り立つ。

もう一度微分すると，
　(左辺)=ｆ''(x)   x=aとすると   (左辺)=ｆ''(a)
であり，
　(右辺)=2p   x=aとしても   (右辺)=2p
(左辺)=(右辺)となるために，
ｆ''(a)=2p でなければならず，
よって，　
      ｆ''(a)　
p= -----　となる。
   　　2！

更に，同様に三次式で近似しようとすると，
     　　　　　　　　　　ｆ''(a)
f(x)≒ｆ(a)+ｆ'(a)(x-a)+-----(x-a)²+q(x-a)³
　　    　　　　　　　　　 2!
とおき，同様の計算をして，　
     ｆ'''(a)
q= ------
　　 3!
となる。

これを４次，５次と続けていくことで，次のテイラー展開を得る。

　　　　ｆ'(a)　　ｆ''(a) ｆ'''(a)　　　　　ｆ''''(a)
f(x)≒ｆ(a)+-----(x-a)+-----(x-a)²+-----(x-a)³+-----(x-a)⁴+…
　　　　　1!　　　　　　 2! 3! 4!

更に，a=0の特殊な場合について考えた次の式を，マクローリン展開という。

　　　　ｆ'(0)　ｆ''(0) ｆ'''(0)　　ｆ''''(0)
f(x)≒ｆ(0)+---- x+----- x²+----- x³+----- x⁴+…
　　　　　1!　　　 2! 3! 4!

である。

　　　さてさて，更にエディタで美しく数式を表現すると，以下のようになります。

いよいよ，仕上げで，動くグラフをどうぞ。サインカーブが，3次式，5次式，7次式，9次式・・・・・とどんどん近似されていきます。