正多面体の美しさについて、図形を多用して考えてみた。
regular polyhedron正多面体(せいためんたい、regular polyhedron)、またはプラトンの立体(プラトンのりったい、Platonic solid)とは、すべての面が同一の正多角形で構成されてあり、かつすべての頂点において接する面の数が等しい凸多面体のこと。正多面体には正四面体、正六面体、正八面体、正十二面体、正二十面体の五種類がある。 三次元空間の中に一つの頂点を取り、その周りに取ることが可能な正多角形に関する制限から、正多面体が先に示した五種類のみであることが証明できる。このことは、オイラーの多面体公式からも証明できる。しかし、条件を緩めることによって、正多面体の拡張を考えることができる(参照:星型正多面体、ねじれ正多面体、正平面充填形)。正多面体の構成面を正 p 角形、頂点に集まる面の数を q として {p, q} のように表すことができる。これをシュレーフリ記号という。シュレーフリ記号は半正多面体(別名:アルキメデスの立体)にも拡張することができる。 これは、wikiから。 きっかけは,平成26年12月の郷中ゼミから,こんな問題が出された。
いっぱい図を作ってみた。 まずこれは,Mathematica10.0のパッケージから。美しいが,そんだけといえばそんだけ。ノートブックファイルはこちらから
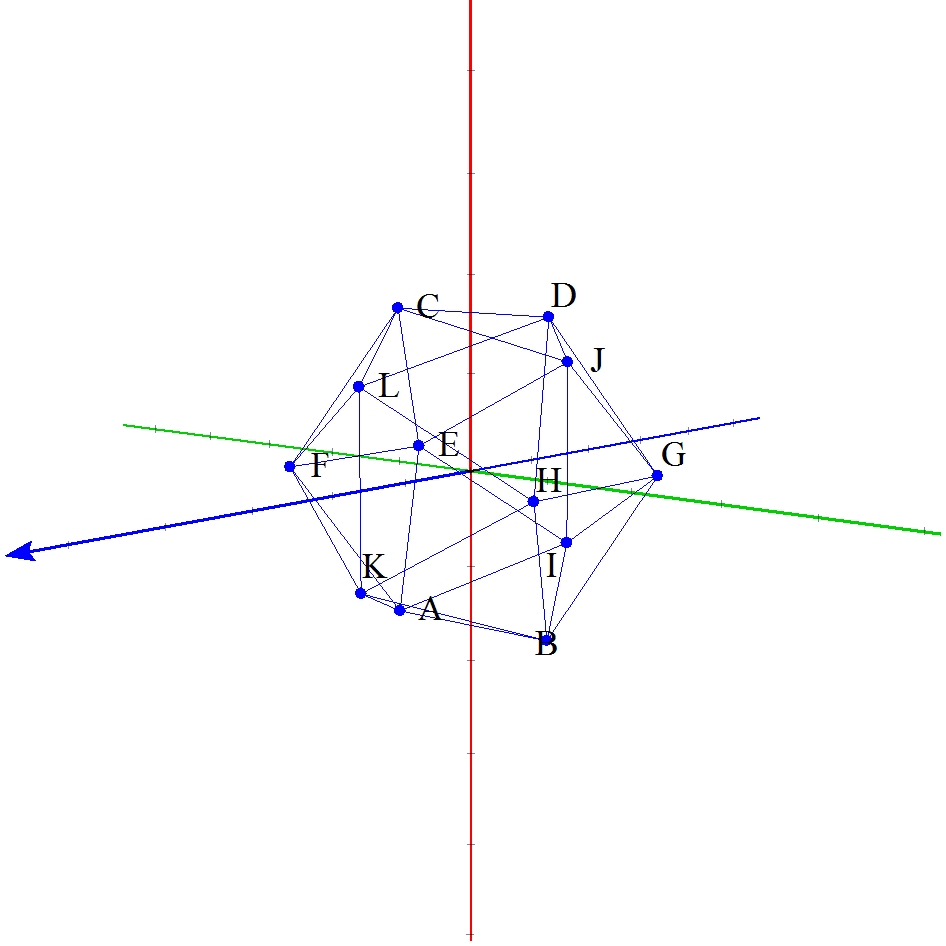
次にあげる,Grapes3Dのほうが,手に持った感じで楽しい。(この座標をとるのが大変!) Grapesファイルは 正12面体のこちら と 正20面体のこちら から
MadMagという磁石のおもちゃで正12面体を作ってみた。美しい!!
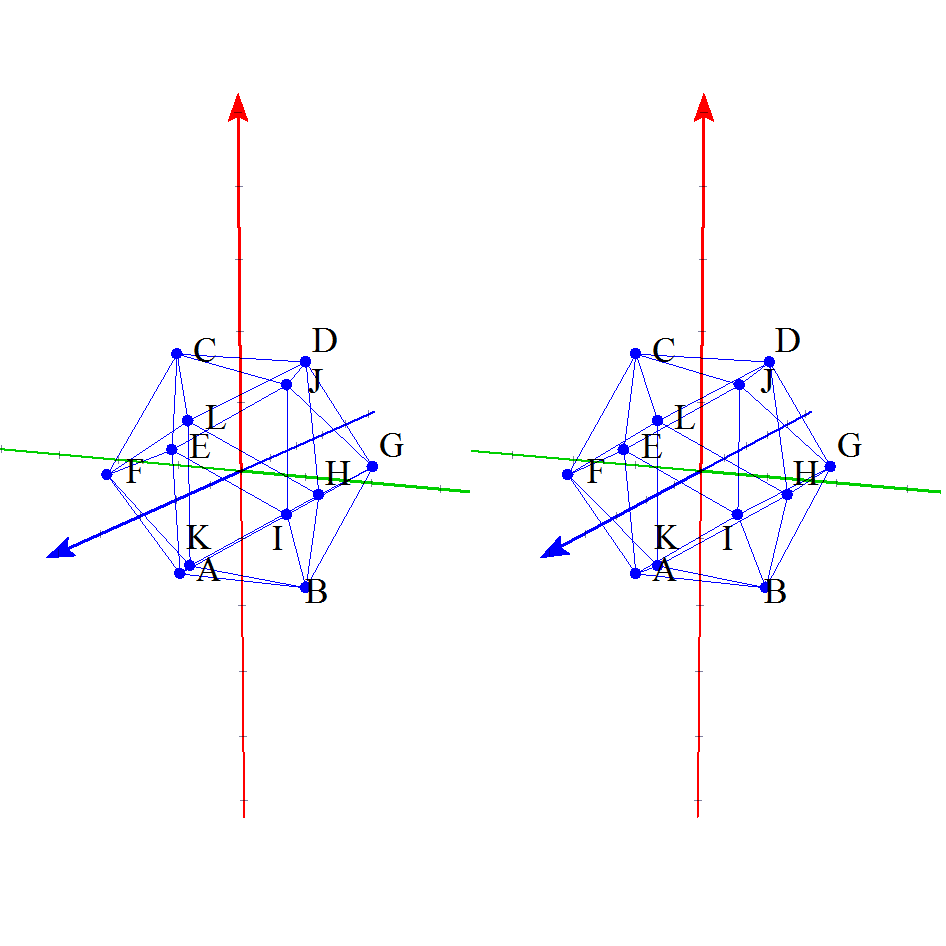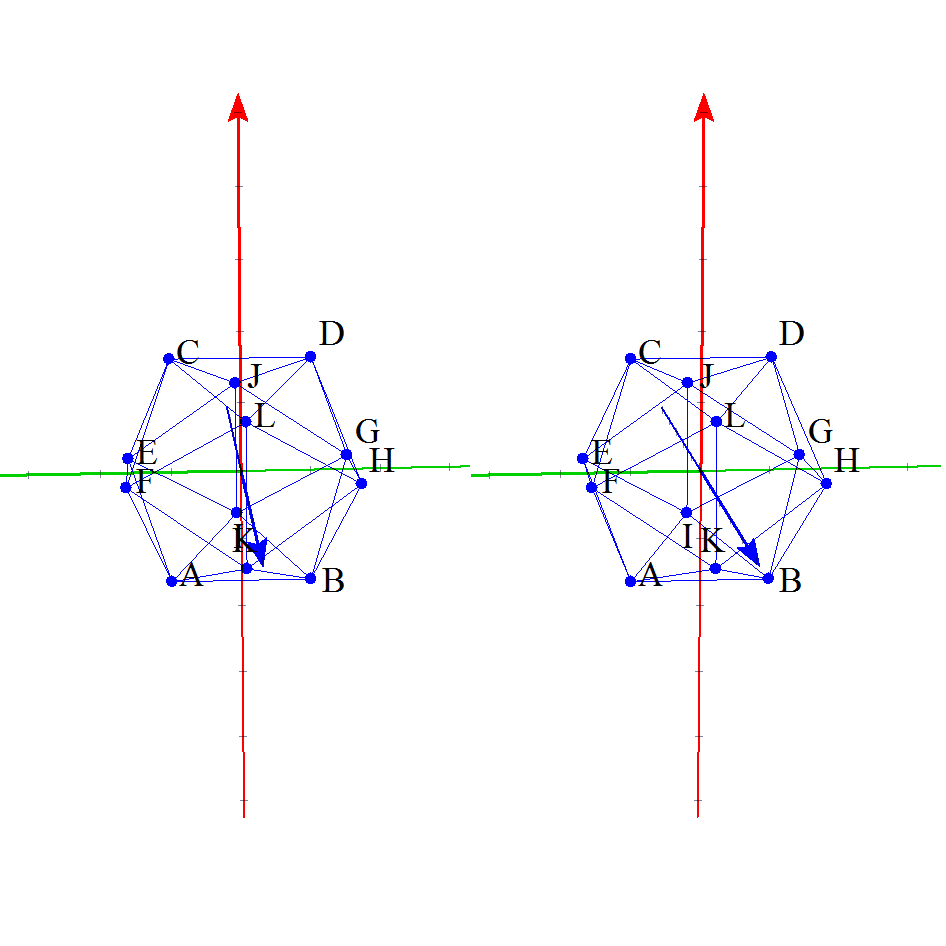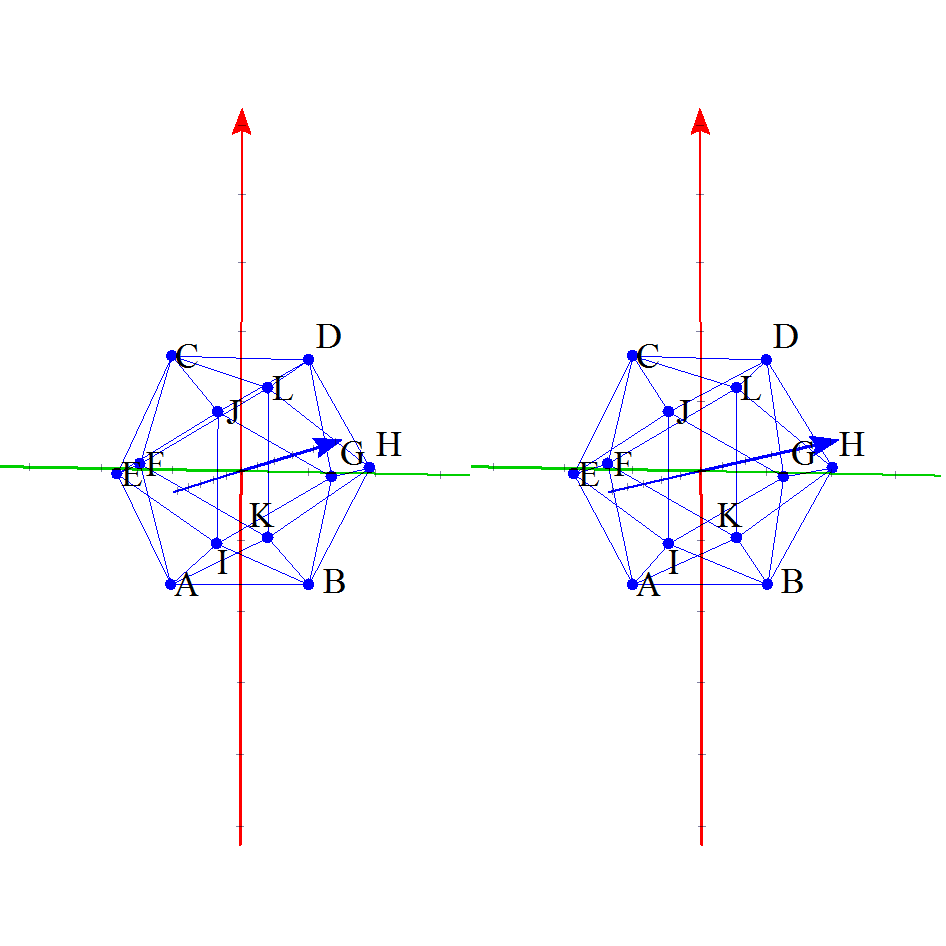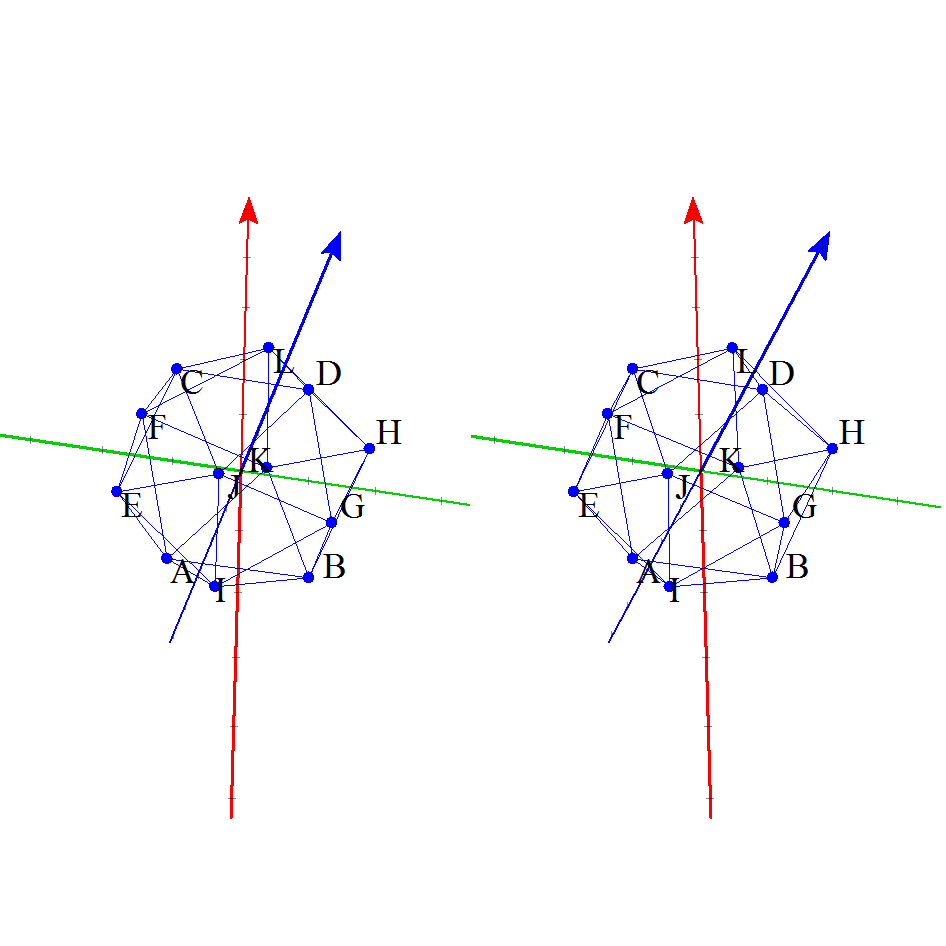
更に,動く数学がコンセプトなので,下の図は,なんと,動いて,かつ,立体視できる!!
ホントは,もうちょっと 座標データとか,東大の問題とかを掲載したかったけど,とりあえず,立体図形がたくさん集まったので(平面だけど) 公開としました。 そのうち,時間を見つけて,入試問題と絡めていきたいと考えています。ごめんなさい。
|
||||||
|
郷中ゼミでの授業がヒントになり、 こつこつと作っていたものを、いよいよ一挙公開!ってまでもないですが、 センター試験も終わって、やっとこさ、落ち着いてきたところなので、書こうかな(まとめとこうかな)?と。 穏やかな日曜日。担任は出願の三者面談で超多忙だが、副担任の私は,(すんません)のんびりと数学をした一日だった。 これから2次に向けて,集中していかねばならない。 そもそも,Grapes3Dは,こちらのサイトからどうぞ。 http://www.osaka-kyoiku.ac.jp/~tomodak/grapes/
|