|
|
|
周上に三点があると,面積はどうなるの??って問題です。 |
(東京工業大学2007年 正八角形の周上の点) 2010.12.19
|
|
|
周上に三点があると,面積はどうなるの??って問題です。 |
さて,いきなりですが,難しさはここに。
| 正八角形の”頂点”に3点があり,三角形を作るならば,ひょっとして中学生向けの問題?ってことになりますが,それがそれ,ここは東京工業大学なんですよね〜。問題は,”周上”の点なんですよ。コレが曲者〜〜〜。 |
さてさて,話は置いといて,頂点上の点で良いということが保障されると,答にはたどり着きやすいです。
以下のようなアニメで,予想が立ちますね。
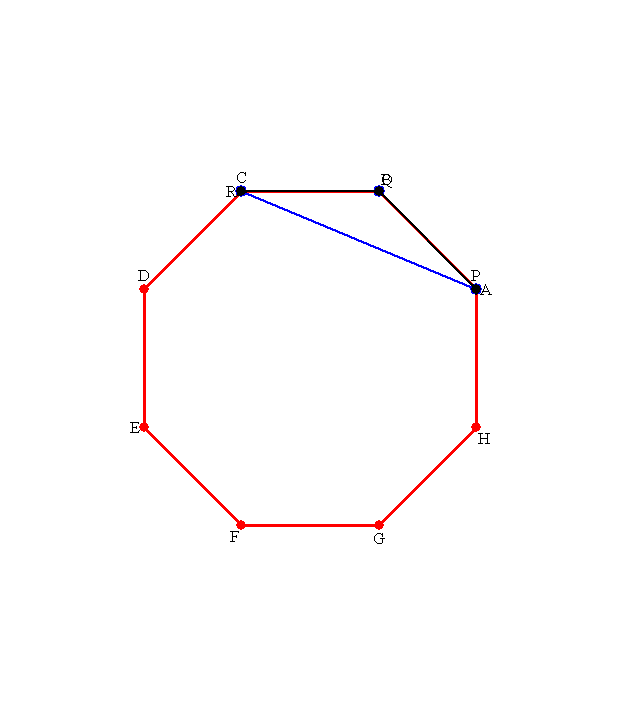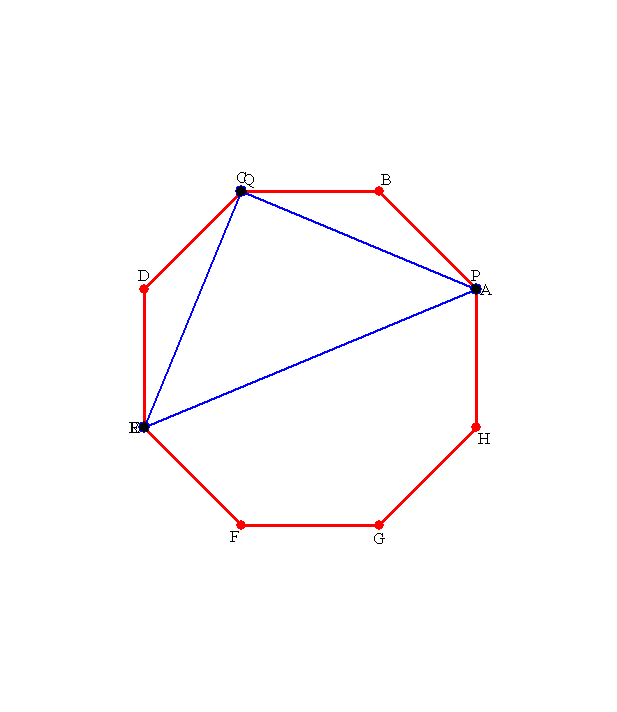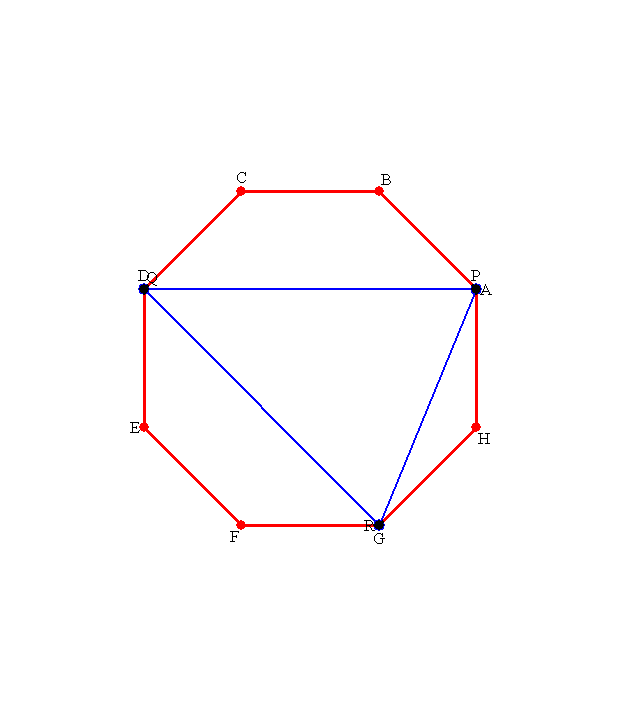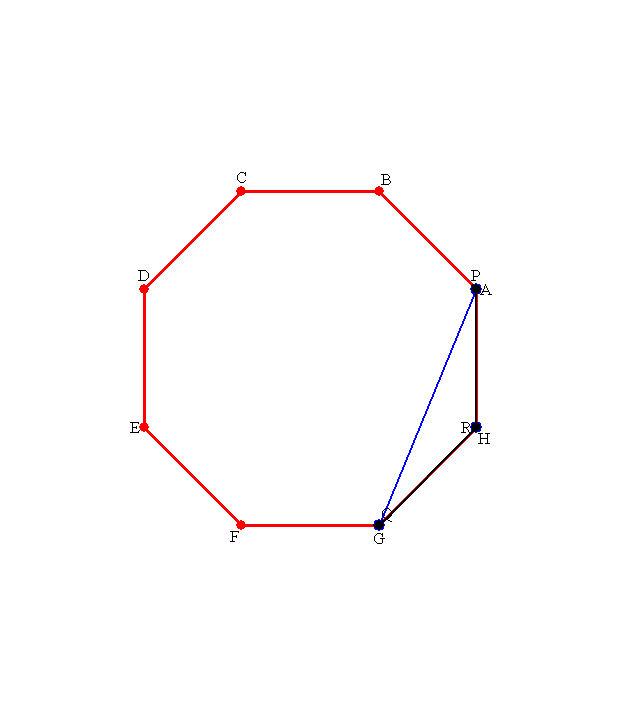 |
ご覧のように,答がイメージできれば解けたも同然です。
この話は,nCr の話ですよね。何個出来るか,何種類出来るか。その中での最大値ってなると,答だけは先に求まる事でしょう。
(もっとも,東京工業大学ではそんなことは想定済みで,答だけはだめ〜,周の頂点上と辺上との差異を答えなければならないでしょう。)
本当の難しさは,下図のような周の辺上に点はいらない!ってことを言う事でしょう。
 この図に この図に |
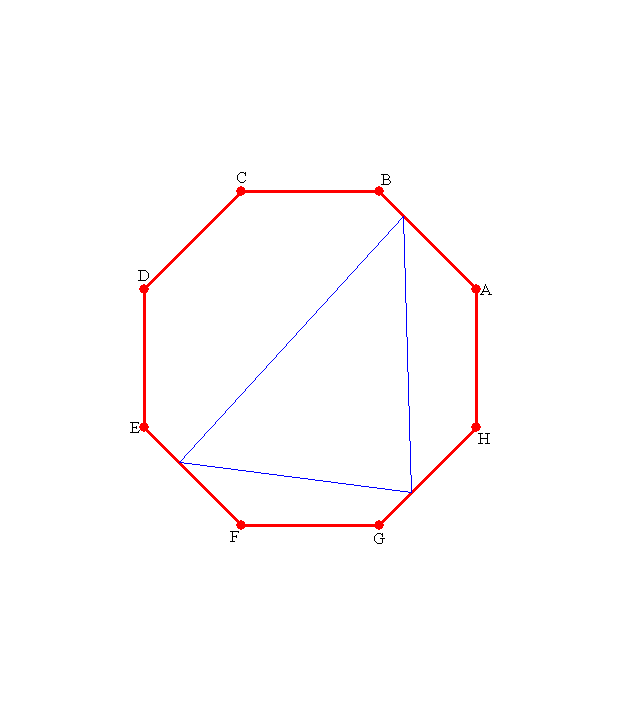 周上の点で三角形を作ると 周上の点で三角形を作ると |
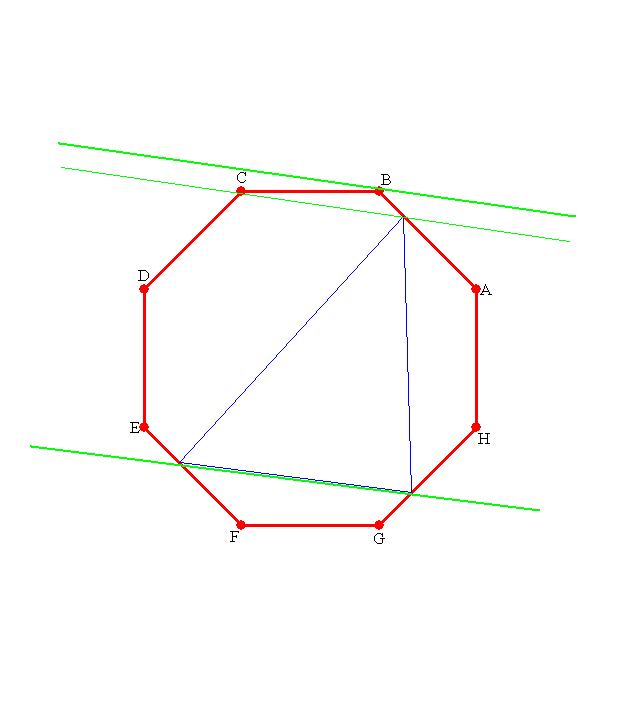 平行線を描くことで,そのサイズよりも面積の大きい三角形が存在するわけです。 平行線を描くことで,そのサイズよりも面積の大きい三角形が存在するわけです。 |
|
【まとめ】 コレを作ったGRAPESのファイルは,こちらからどうぞ。 (右クリックしてファイルを保存してからの方が扱いやすいかも?) こんな感じのファイルです。
本日参観した授業でテーマとして扱われた問題です。なかなか簡単そうで,説明が難しいところです。言葉で書くのは無理がありそうなので,図をいっぱい書いて,その横に説明を一言加えるだけで,得点になると思われますが,大学の先生方,いかがでしょうか? 三角形の頂点が正八角形の頂点にあれば,ホントに高校入試問題にも使えそうです。でも,東工大の採点基準では,答えはあってるが・・・という解答はほとんど,0点かもしれませんね。 おまけ, 八角形という語をローマ字入力するために,HAKKAKKEIと打つわけだが, 何度間違えて,HAKKAKEIと打ったことか。Kが足りない〜Kが多すぎ〜 こう打つと,”発火系”と変換されて悲しい。。。(T_T)
|