なんだか，今日（2/28の日曜日）は，意外に時間がぽっかりと空いて，ほんじゃ東大の問題でもちょっと見てみるか，ってやり始めたら，この理系３番が，あ，こりゃGrapes3Dの出番だ！ってことで作り始めて，いま30分ぐらいたったところです。

こんな問題でして，

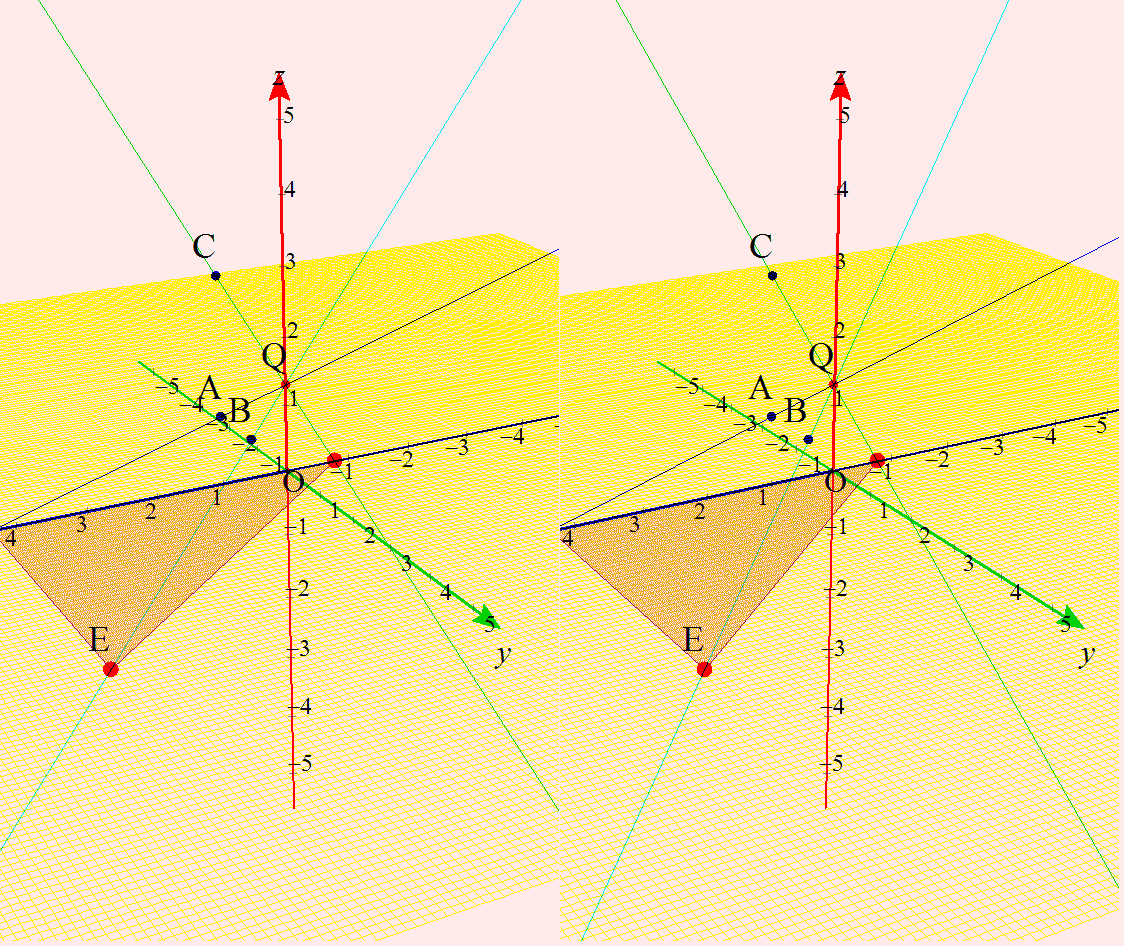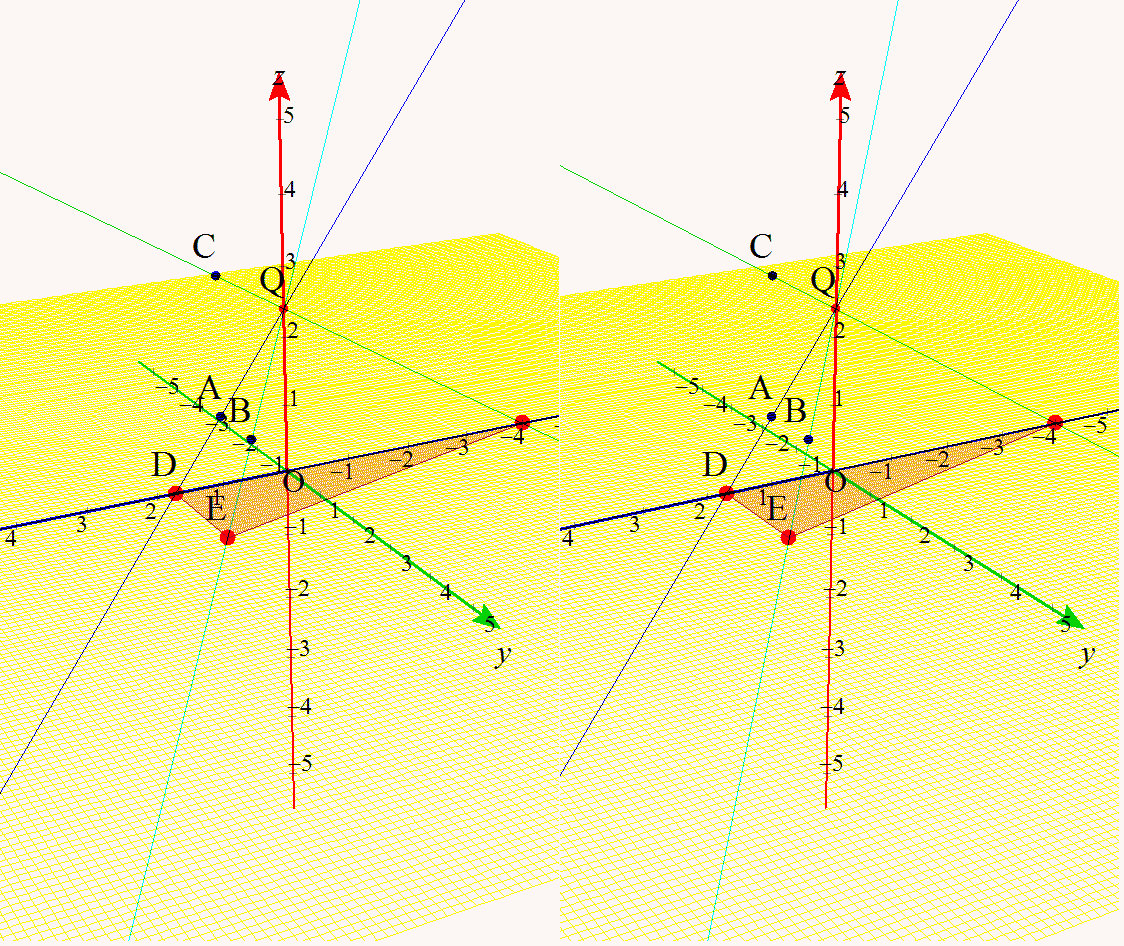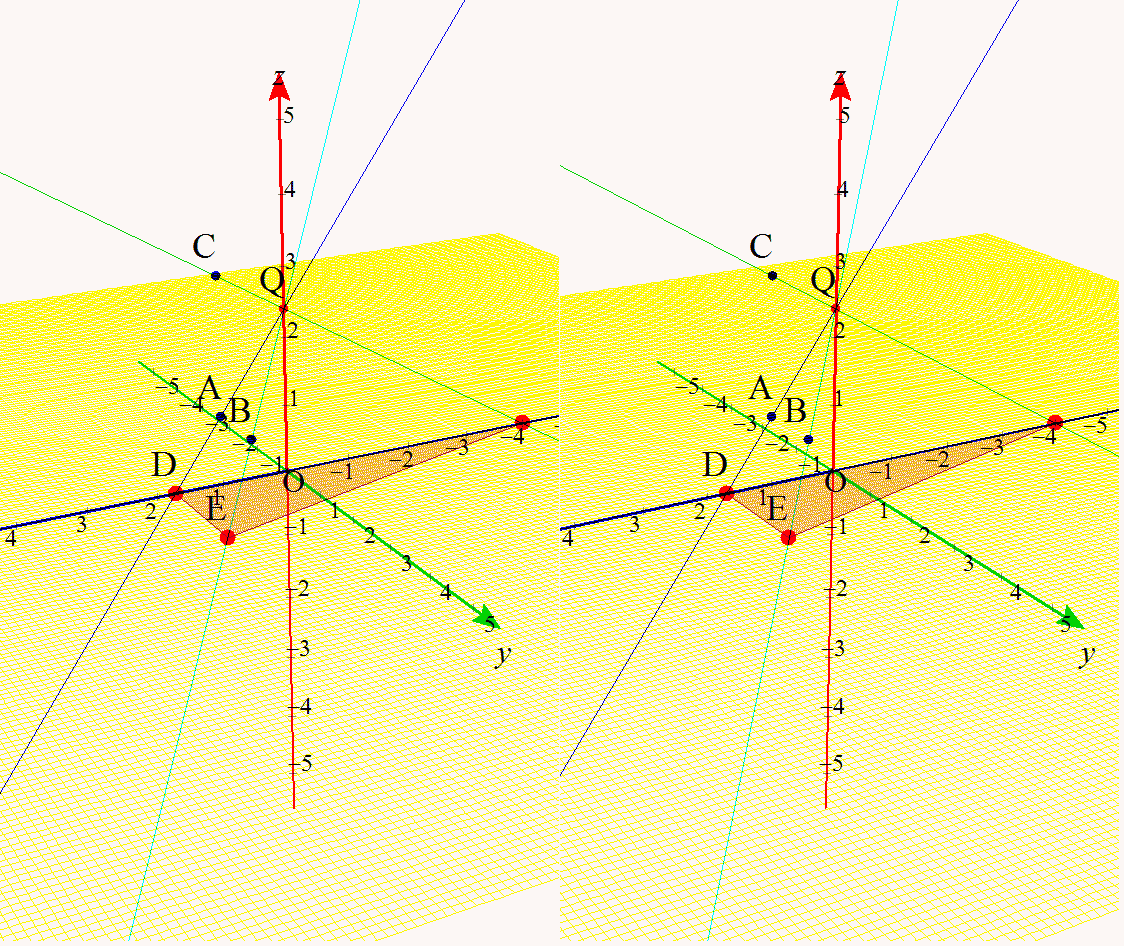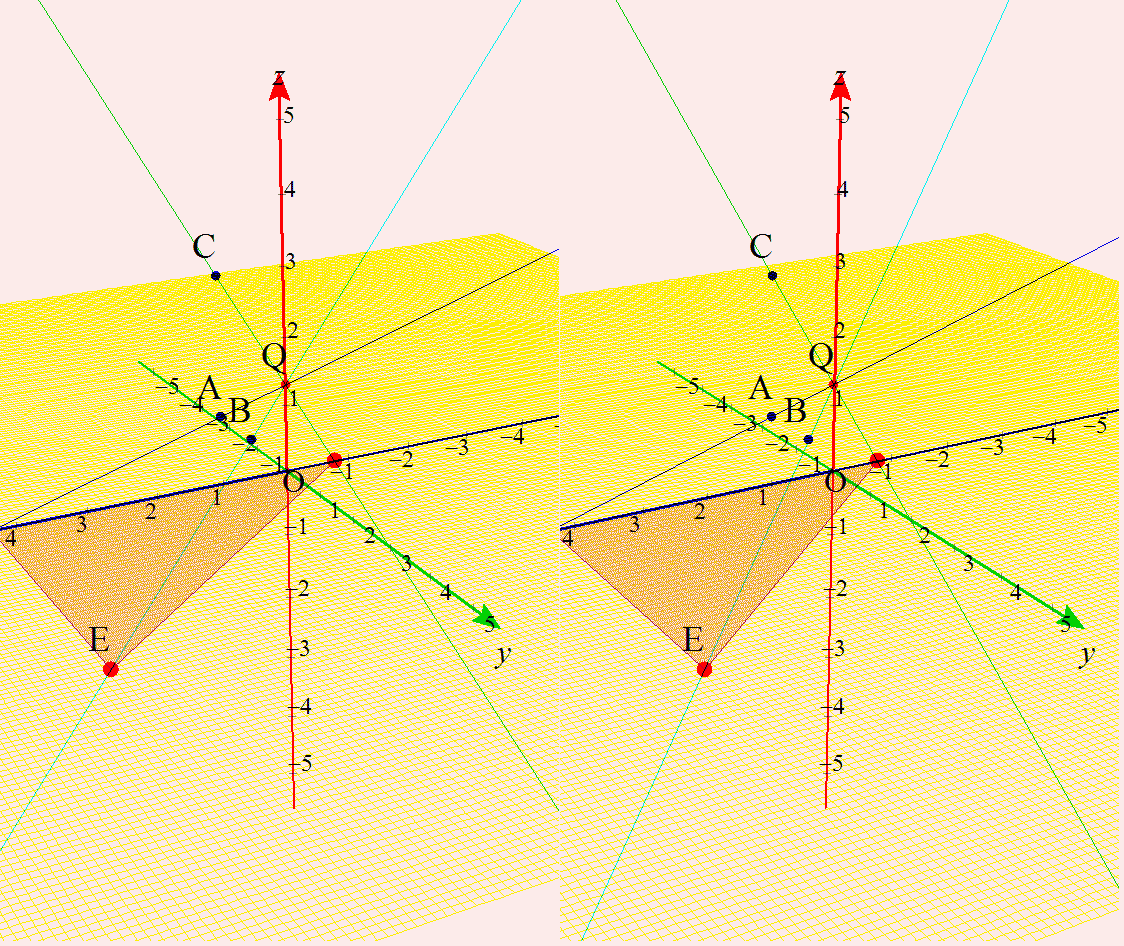
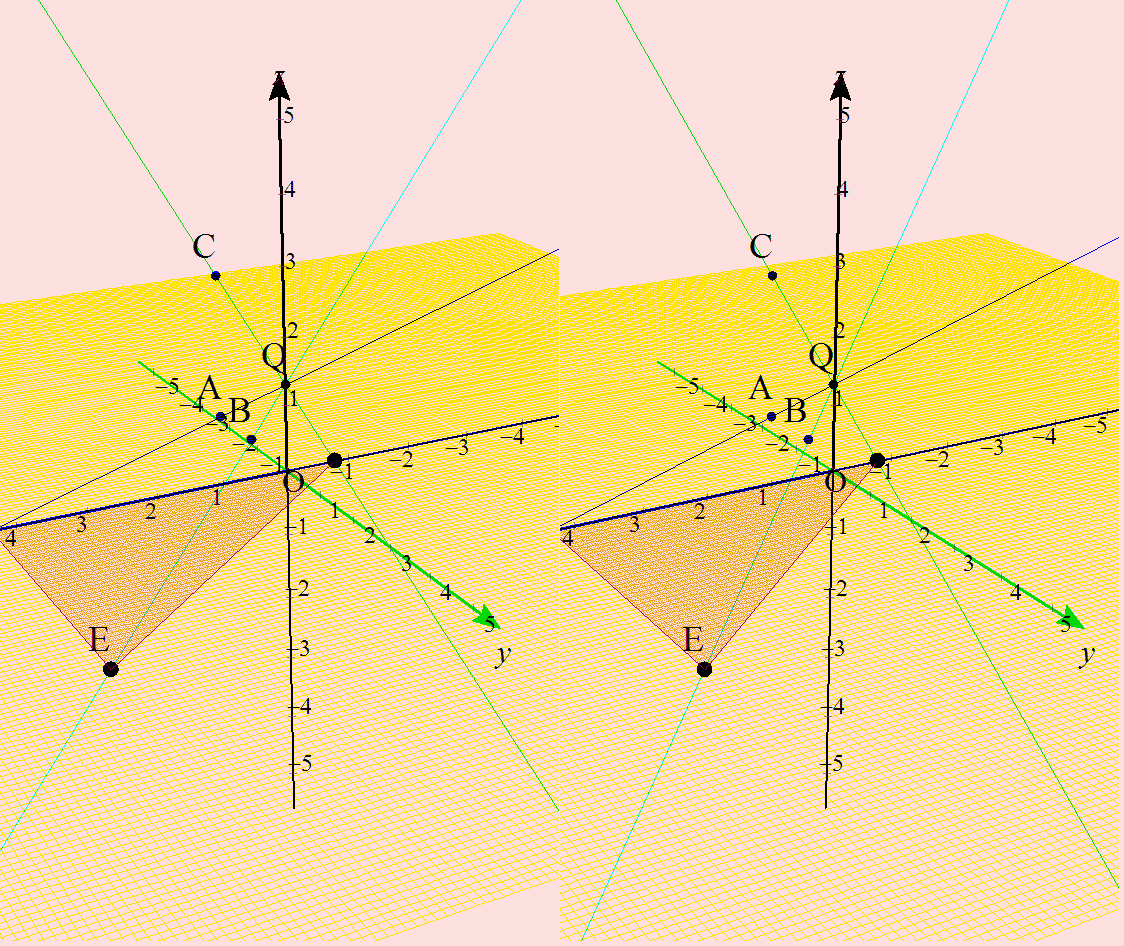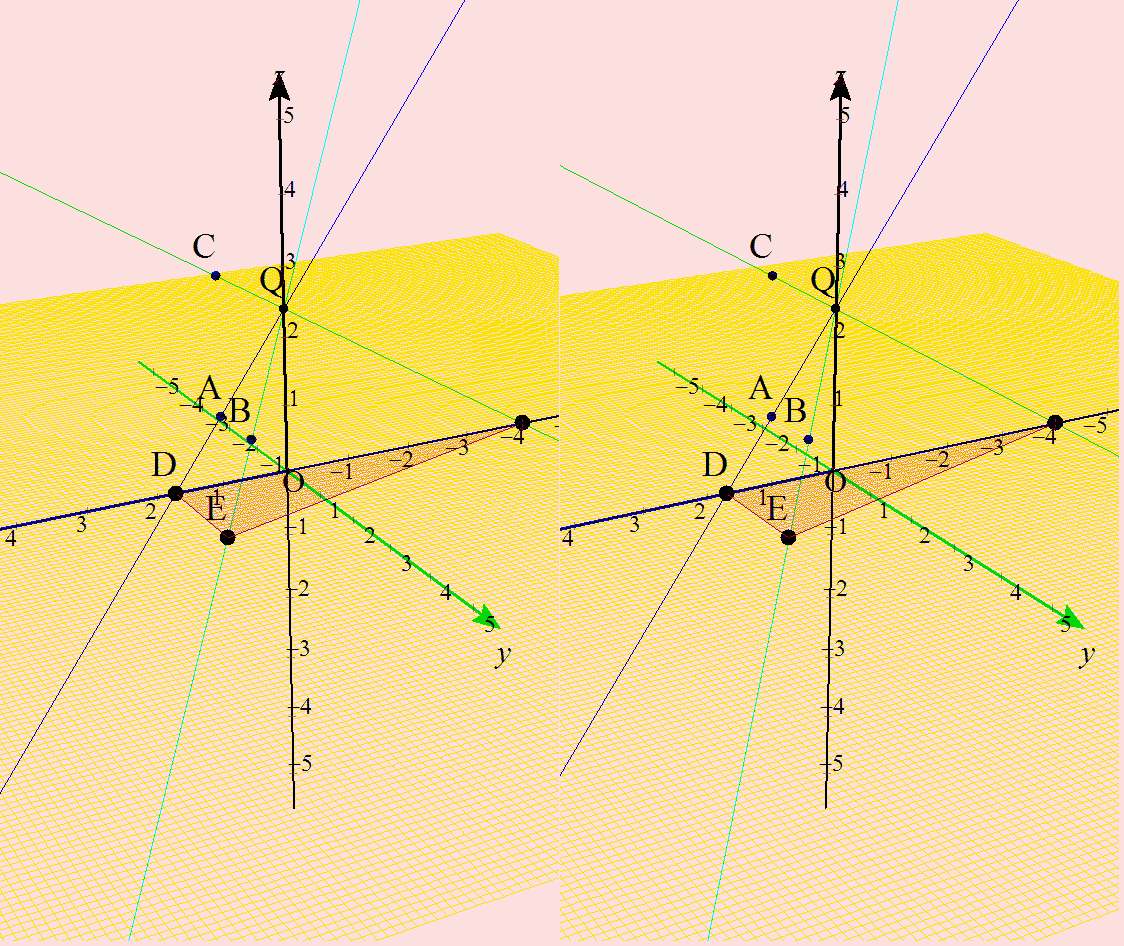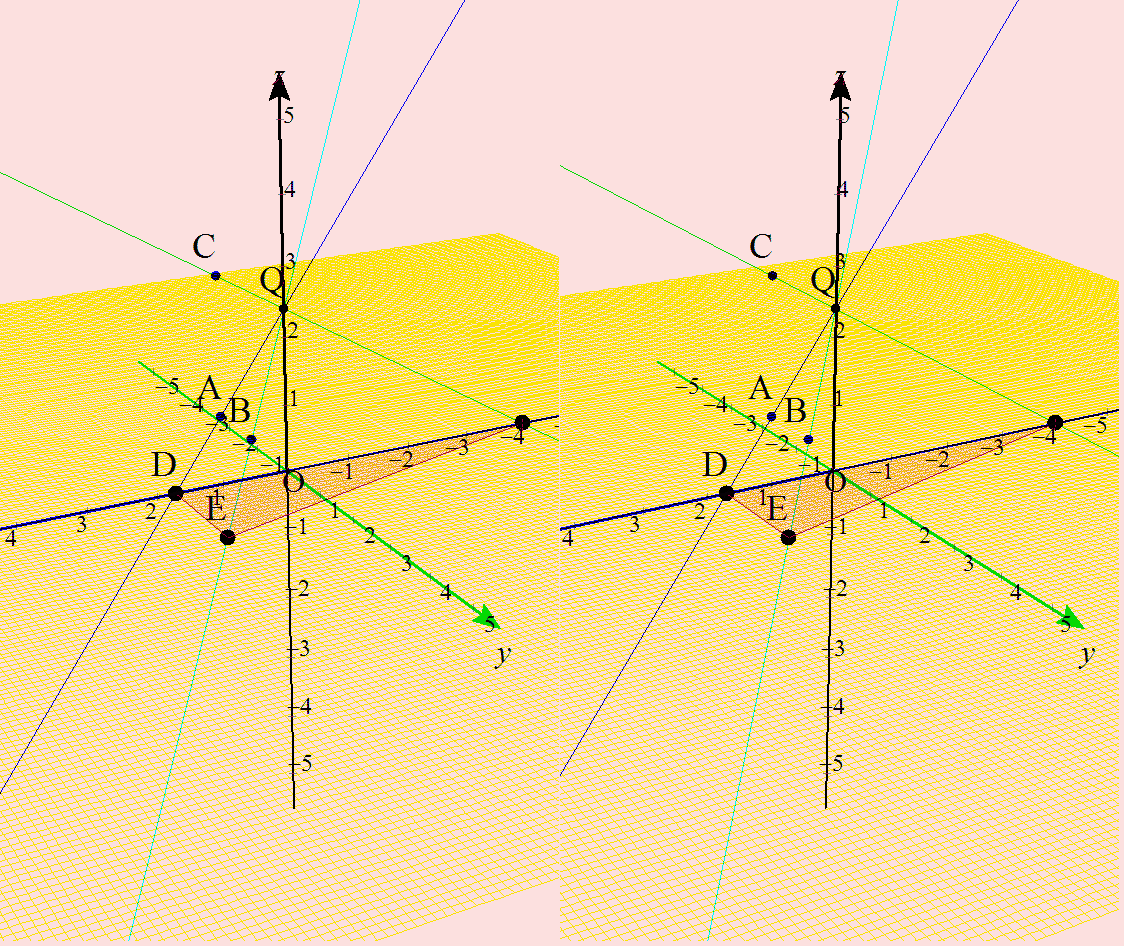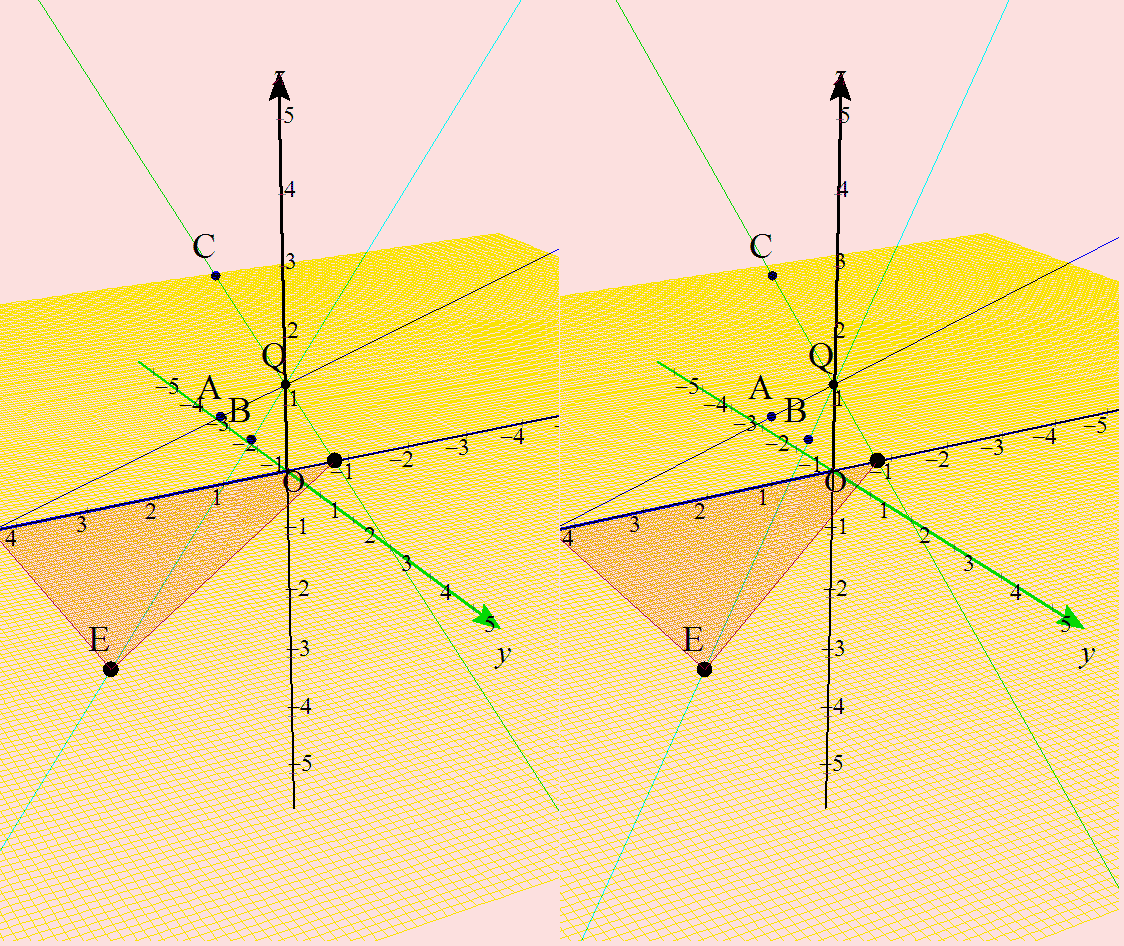
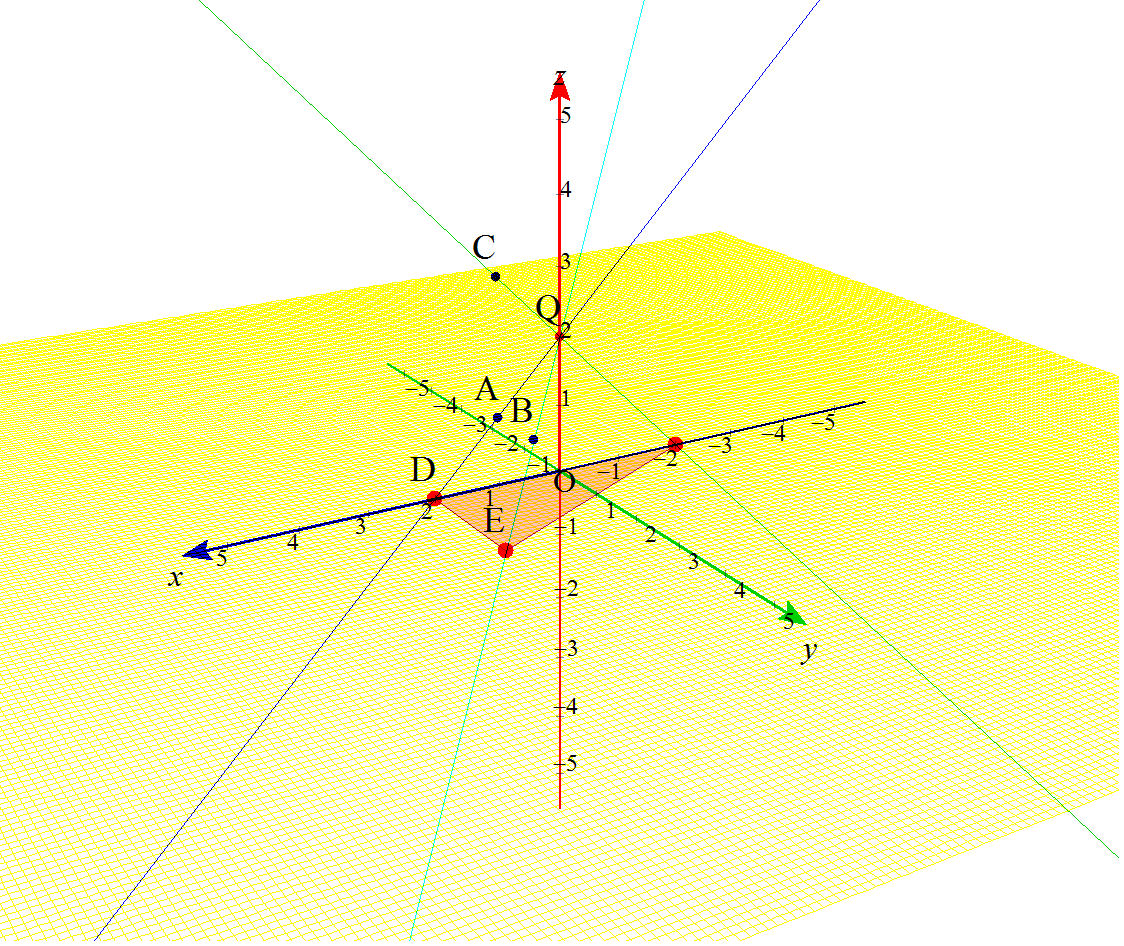
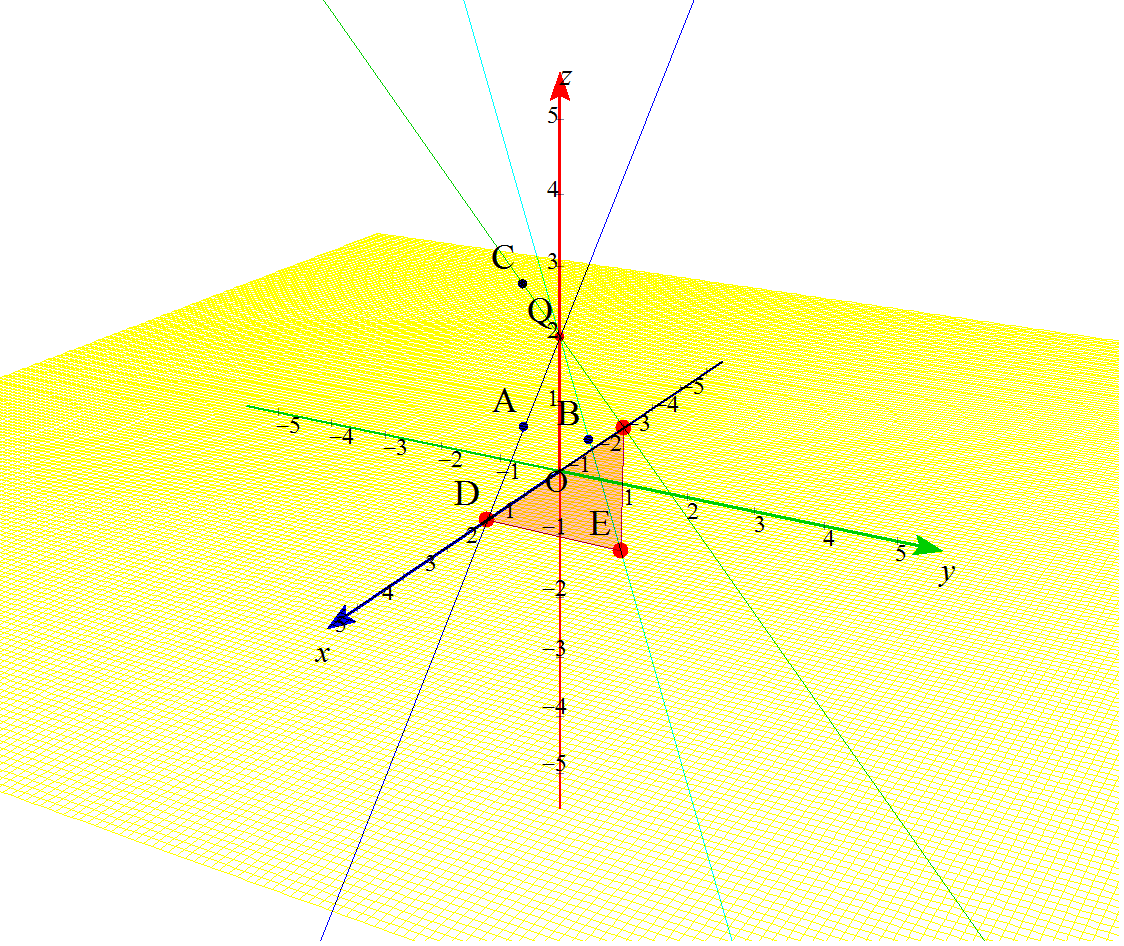
という，空間ベクトル内の，動点と三角形の面積（微分）との融合問題といったらいいのでしょうか？

いつものように，詳しい解答は載せていません。直線の方程式をベクトル表示で作り，ｘｙ平面との交点なのでz=0とし，三角形が直角三角形ということが分かると，求積をするが，最大最小は，その面積関数の微分で与えられるよね。って話です。でも，イメージ先行型で，答え予想が出来ちゃうところが面白いですね。

なんだか，昔（というか毎年？）見かけるような，いろんな分野との融合の，「立体イメージを持ってるか諸君！」って，教授ら怒られてる感じがする問題ですね。

僕はこれは，

「１．立体イメージつくれるか？
　２．答え予想できるか？
　３．正しく微分計算できるか？」
と問われている気がします。

さて，早速，これをGrapes3Dで描いてみたのが，これです。

ホントなら，ここにアニメを掲載するところだけど，ちょっと立体視したほうが面白そうだったので，大きめサイズになりました。そのため下のほうに掲載しました。そちらを見てください。

【解説】

【おまけ】

　ご覧になるとどうでしょう？明らかに，a=2が答えっぽいですよね。なぜなら，ｚ座標z=1とz=3の中点だったとき，ｘ軸上の三角形の長さとしては，最短になりますもんね。

↑この上の記述ですが，間違っておりました。<m(__)m>（2016.3.6）　　

　ｘ軸上の三角形の底辺にあたる部分，僕の図なら線分DFにあたる部分ですが，少し違和感を感じて，再度計算をやり直したところ，√3のときが，最短にあたることが分かりました。三角形の高さにあたる部分，僕の図なら線分DEですが，こちらは単調減少してるのですが，（底辺）×（高さ）÷２で三角形の面積を出す際に，両方の組み合わせでバランスをとり，√3ではなく，2のところで面積最小になることが分かりました。問題としてはそんなに単純ではなく，絶妙なバランスの上に成り立っていることが分かりました。問題としては，平面上の線分の長さが最短となるaは？と聞かれたら，a=√3というこっちはこっちで面白い問題になると思われます。

丁寧に解くことで完答されるべき問題であると思います。

さてさて，最後に，そのアニメーションの作成について書いておきます。

Grapes3Dで作図する。（ファイルはこちらからどうぞ）
パラメータを変えながらGIFで連番出力する。
GiamでGIFアニメーションへの処理をする。

やっぱりテクニックはこれだけでした。