|
基本的には,三角形の図形の処理と∑計算と極限練習のような,計算問題の体をなしているようです。
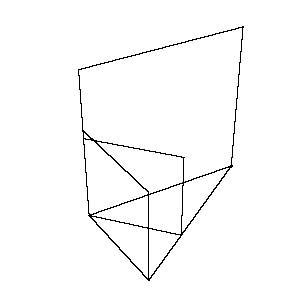
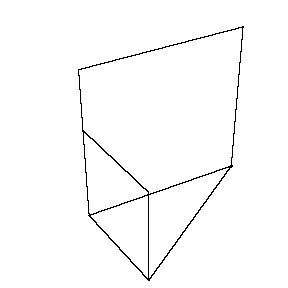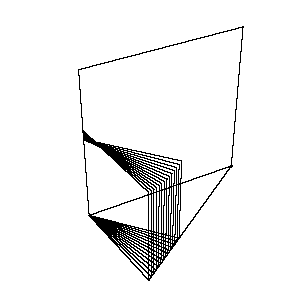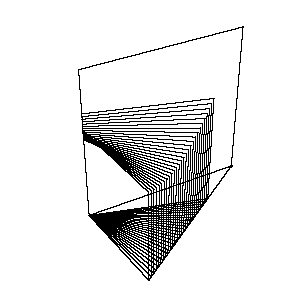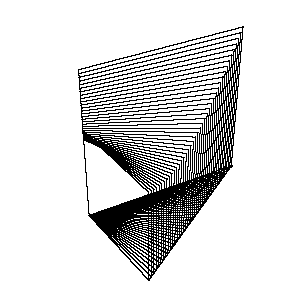
図形的な意味としては,
△ABCにおいて辺BC上を動く動点Pがあって,
一辺をAPとする正方形を描いていくときに
作る立体の体積を区分求積法で求めた。
ということになりますね。
アニメを作ってみたのがこちら。
実際にMathematicaで作図してみて思ったのは,
あんまり意味無い立体かなぁ~残念。。というところです。
実際にはちょっとあり得そうも無く,使えそうも無いのかもしれません。
ま,数学的には面白く,上部は緩やかな曲線を描き,
性質的には区分求積による積分でしか求めようが無いかもしれません。
計算してみると,まぁまぁキレイな解が出たので,美しい部類には入ると思います。
とにかく計算出来るから,計算してみてね。と言うような性質でしょう。
実際にこの立体が作られる様子をご覧下さい。アニメで動くと,脳内イメージが固定化できますね~
質問いただいた掲示板はこちらから。
http://geocities.yahoo.co.jp/gb/sign_view?member=bassfishiing

【作図方法のメモ】
一般的な文字では作図できなかったため,座標を以下のように固定して作成した。
原点(0,0,0)を三角形の頂点Aとして,
B(2,-1,0),C(2,3,0)とし,
辺BCがy軸と平行にx=2の直線上を動く点Pがある
と考えた。
更に,点Pのy座標が,-1<=y<=3と変化する間に,
Pの鉛直上にz=√2^2+y^2と計算させ,
そこに,APを一辺とする正方形を描いた。
う~ん書いててこれでは伝わらないかもしれないと思ったので,
Mathematicaのnbファイルを,テキストと画像とソース全部
載せておく事にした。ちょっと恥ずかしいが,ま,この程度の力しか
持っておりませぬ。。。
Mathematicaのノートブックファイルは,こちらからどうぞ。
Do[
z := Sqr[(2^2 + y^2)];
p1 = Line[{{0, 0, 0}, {2,-1, 0}, {2, 3, 0}, {0, 0, 0}}];
p2 = Line[{{0, 0, 0}, {2, y, 0}, {2, y, z}, {0, 0, z}, {0, 0, 0}}];
p3 = Line[{{0, 0, 0}, {2,-1, 0}, {2,-1, Sqr[5]}, {0, 0, Sqr[5]}, {0, 0,
0}}];
p4 = Line[{{0, 0, 0}, {2, 3, 0}, {2, 3, Sqr[13]}, {0, 0, Sqr[13]}, {0,
0, 0}}];
p5 = Point[{2, 3, 0}];
Show[Graphics3D[{p1, p2, p3, p4, p5}, Axes -> False, Boxed ->
False]], {y,-1,3,0.1}
]

|
【Mathematicaとアニメ処理の備忘録メモ】
Line命令で三角形のフレームを描く。
Do命令でyを変化させ,それに同調する形でzを計算させ,
新たなLineが次々に引かれるようにしてある。
Save as HTMLでファイルを書き出す。
GiamでBMPを読み込み処理する。
元々のMathematicaでは,少しずつずれた正方形を
描いているので,Giamで背景の白色のみを消去させて,
ずれながらもそれまでの正方形が残像のように残るように
処理したものがGIFアニメである。
| なんとなんと。。。後日談(2012.9.19追記)
ぱらぱらと,先日,東京大学入試問題50年という本を眺めていたら,この問題の出展は,「ここ」にあったことが判明した。な~~んだ東大だったわけね。。。。ややこしい計算をさせる人だ・・・・怪しげな中華問題というタイトルをつけたけど,元のもともとは,東大の1978年(昭和53年)の入試問題を,中国で練習問題に出しただけ,というものだった。
それにしても,この質問者のbkさんは,分かってて出したのか,知らずに出したのか,それにしても,コタエは出てしまったなんて,すっげーじゃん,というか,解答掲載して,もう3年ぐらいになるけど,多分,お礼というかお返事というか,なーんにもなくて寂しいや。。。。
へぇ,,,昔,東大こんなの出してたのね~~~~

|
BACK
|