乮俋俋丂幁帣搰戝丂係乕俀乯
丂兛亖cos(俈俀並)亄倝sin(俈俀並)偲偍偔偲偒丄師偺栤偵摎偊傛丅
丂偨偩偟丄倝偼嫊悢扨埵偲偡傞丅
(1)摍幃(倶亅侾)(倶係亄倶俁亄倶俀亄倶亄侾)亖倶俆亅侾偑惉傝棫偮偙偲傪帵偣丅
(2)兛偼曽掱幃倶俆亖侾偍傛傃丄倶係亄倶俁亄倶俀亄倶亄侾亖侽偺夝偲側傞偙偲傪帵偣丅
傑偨丄 傪嬌宍幃傪梡偄偰昞偣丅
侾
----
丂 兛
(3)
侾
兝亖兛亄----偲偍偔偲偒丄(2)傛傝兝偼曽掱幃倶俀亄倶亅侾亖侽偺夝偲
兛
側傞偙偲傪帵偟丄偙傟傪梡偄偰丄
嚂俆亅侾
嚂侾侽亄俀嚂俆
丂cos(俈俀並)亖---------- 丄sin(俈俀並)亖--------------
係
丂係
偲側傞偙偲傪徹柧偣傛丅
亂夝愢亃
丂
(1)偼悢妛俙偺幃偺揥奐偱偁傞丅2師偵弌戣偡傞偺偼偳偆偐偲偄偆堄尒傕偁傞偐傕偟傟側偄偑丆庴尡惗偵偲偭偰丆傎偭偲堦懅偮偔丆摫擖偲偟偰偼椙偄栤戣偲巚傢傟傞丅
媡偵丆偙傟偑弌棃側偄偲崌奿偼弌棃側偄偩傠偆丅乮偙傟偑夝偗側偄恖偼庴尡偟偰側偄偼偢両乯
(2)(3)偼丆恾宍揑偵偼暋慺悢暯柺忋偺惓屲妏宍偺栤偄偱偁傞丅
嫵壢彂偵傕偙偺栤偄偱偄偆偲偙傠偺兛傑偱偼嵹偭偰偄傞偺偱丆尒妎偊偁傞乽傛偟偭乿偲偄偆庴尡惗傕懡偐偭偨偺偱偼側偐傠偆偐丅
尒偨偙偲偑柍偔偰傕丆徹柧偲偟偰偺弌戣偱偁傞偨傔丆椡媄偱夝偵嬤偯偗偨偱偁傠偆丅
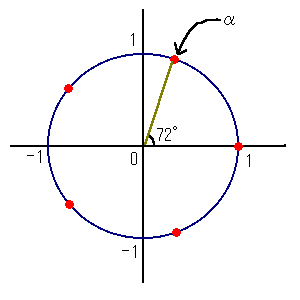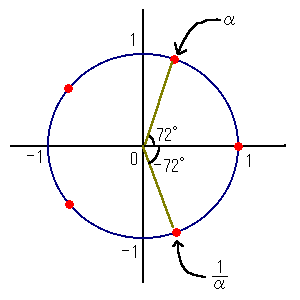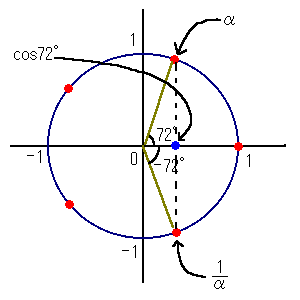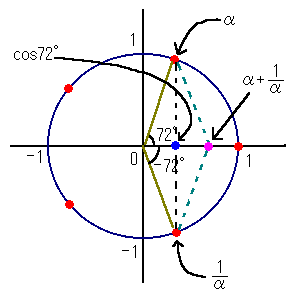
塃恾偼偙偺栤戣偺丆cos72亱偺恾宍揑昞尰丅
sin72亱傕丆徣棯偟偰偄傞偑埲壓偺傛偆偵恾宍揑昞尰偱偒傞丅
丂丂丂丂 1
丂兛亅----亖俀sin72亱偲偟偰丆嫊幉忋偵暯峴巐曈宍傪嶌傞丅
丂丂丂丂 兛
|
 |
亂夝亃
(1)嵍曈傪揥奐偟偰丄塃曈偲摨偠偵側傞偙偲傪寁嶼偡傟偽傛偄乮妝彑両棯乯
(2) 兛亖cos俈俀並亄倝sin俈俀並
侾
侾
丂丂丂亖cos(俁俇侽並亊--- )亄倝sin(俁俇侽並亊---丂)丂
俆
俆
侾
---
亖乮cos俁俇侽並亄倝sin俁俇侽並乯
俆
侾
---
丂 亖侾 俆丂丂丂
丂椉曈傪俆忔偟偰
丂丂兛俆亖侾偲側傝丄兛偼倶俆亖侾偺夝偱偁傞丅
丂偙偙偱(1)偺寢壥傛傝
丂丂兛俆亅侾亖侽偼
丂丂(兛亅侾)(兛係亄兛俁亄兛俀亄兛亄侾)亖侽丂兛亗侾傛傝
丂丂丂 兛係亄兛俁亄兛俀亄兛亄侾亖侽偱偁傞丅丂
偮傑傝兛偼丄倶係亄倶俁亄倶俀亄倶亄侾亖侽偺夝偱偁傞丅
丂傑偨丄
侾
侾
----亖------------------------
兛
cos俈俀並亄倝sin俈俀並
侾 亊(cos俈俀並亅倝sin俈俀並)
亖-------------------------------------
(cos俈俀並亄倝sin俈俀並)亊(cos俈俀並亅倝sin俈俀並)
cos俈俀並亅倝sin俈俀並
亖------------------------
cos俀俈俀並亄sin俀俈俀並
亖cos俈俀並亅倝sin俈俀並 丂丂丂丂丂丂丂丂仼偙傟偼傑偩嬌宍幃偲偼尵偊側偄丅
丂丂丂丂丂丂亖cos(亅俈俀並)亄倝sin(亅俈俀並) 丂丂丂仼偙偺宍傑偱丅栤戣偺(俈俀亱)偼偙傟傪楢憐偝偣偨偐偭偨偺偐丠
(3)倶係亄倶俁亄倶俀亄倶亄侾亖侽ゥゥ@丂偺椉曈傪倶俀偱妱傞偲丄
侾 侾
倶俀亄倶亄侾亄----亄-----亖侽
倶 倶俀
侾
侾
丂乮倶俀亄俀亄-----乯亄乮倶亄----乯亅侾亖侽
倶俀
倶
侾
侾
丂乮倶亄----乯俀亄乮倶亄----乯亅侾亖侽
倶
倶丂丂丂 丂丂丂丂 嘆偺夝偑丄兛偩偐傜丄
1
侾
乮兛亄----乯俀亄乮兛亄----乯亅侾亖侽
兛
兛丂丂丂丂丂丂
傛偭偰
丂丂丂兝俀亄兝亅侾亖侽
偮傑傝丄兝偼倶俀亄倶亅侾亖侽ゥゥA偺夝偱偁傞丅
偙偙偱丄
侾
兝亖兛亄----丂丂偼丄(2)傛傝
兛
亖(cos俈俀並亄倝sin俈俀並)亄(cos俈俀並亅倝sin俈俀並)
丂丂丂丂丂亖俀cos俈俀並亜侽
傑偨丄嘇傪夝偔偲
亅侾亇嚂俆
嚂俆亅侾
丂倶亖-----------丂兝亜侽傛傝丂兝亖----------
俀
俀
廬偭偰丄
嚂俆亅侾
嚂俆亅侾
俀cos俈俀並亖----------
備偊偵丄cos俈俀並亖----------
俀
係
傑偨丄
丂侽亙sin俈俀並亙侾偩偐傜丄
丂sin俈俀並亖嚂侾亅cos俀俈俀並
嚂俆亅侾 丂丂
亖嚂侾亅(---------)俀
係
嚂侾侽亄俀嚂俆
亖---------------
丂丂係
