|
左と右を 両側から |
|||
 |
最上段左図の拡大図
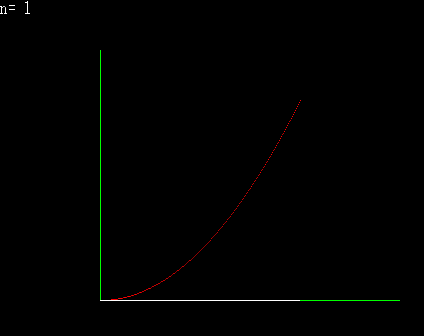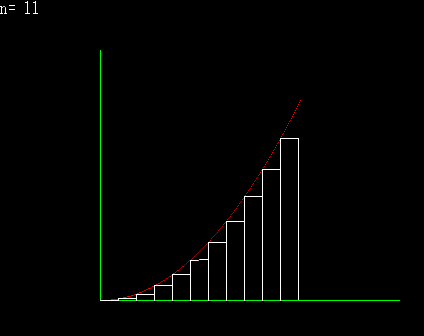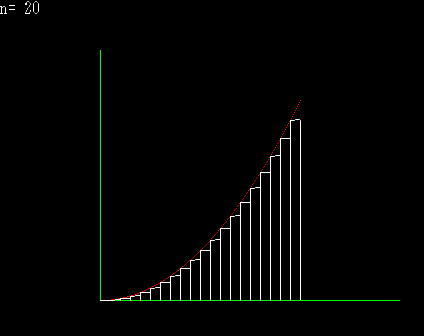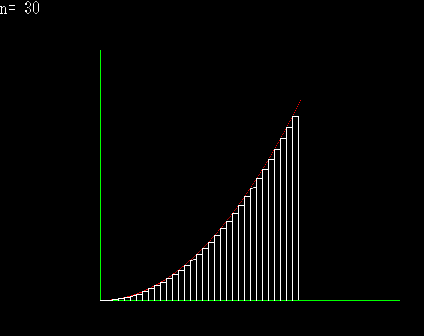
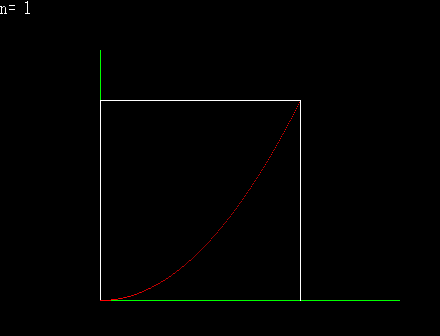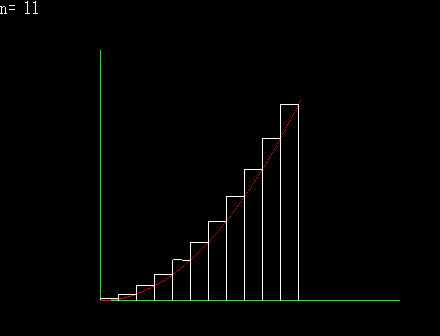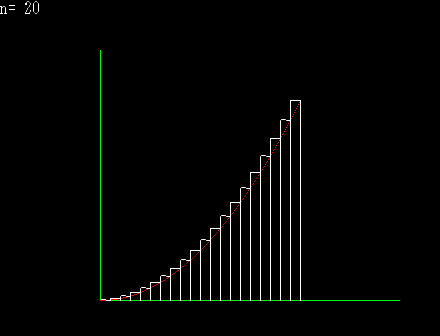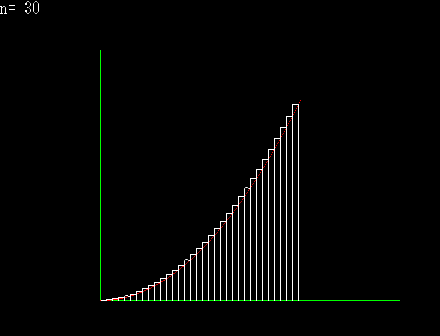
下側から近似してゆく |
|||
 |
最上段右図の拡大図
上側から近似してゆく |
|||
|
この右側の原稿は,授業で活用できるプリントです。印刷してご利用下さい。⇒ |
解説・配布用プリント原稿 | |||
| 2014.11.10追記 この右側の原稿は,更に授業で使いやすく作り直しました。⇒ | 解説プリント原稿PDF | |||
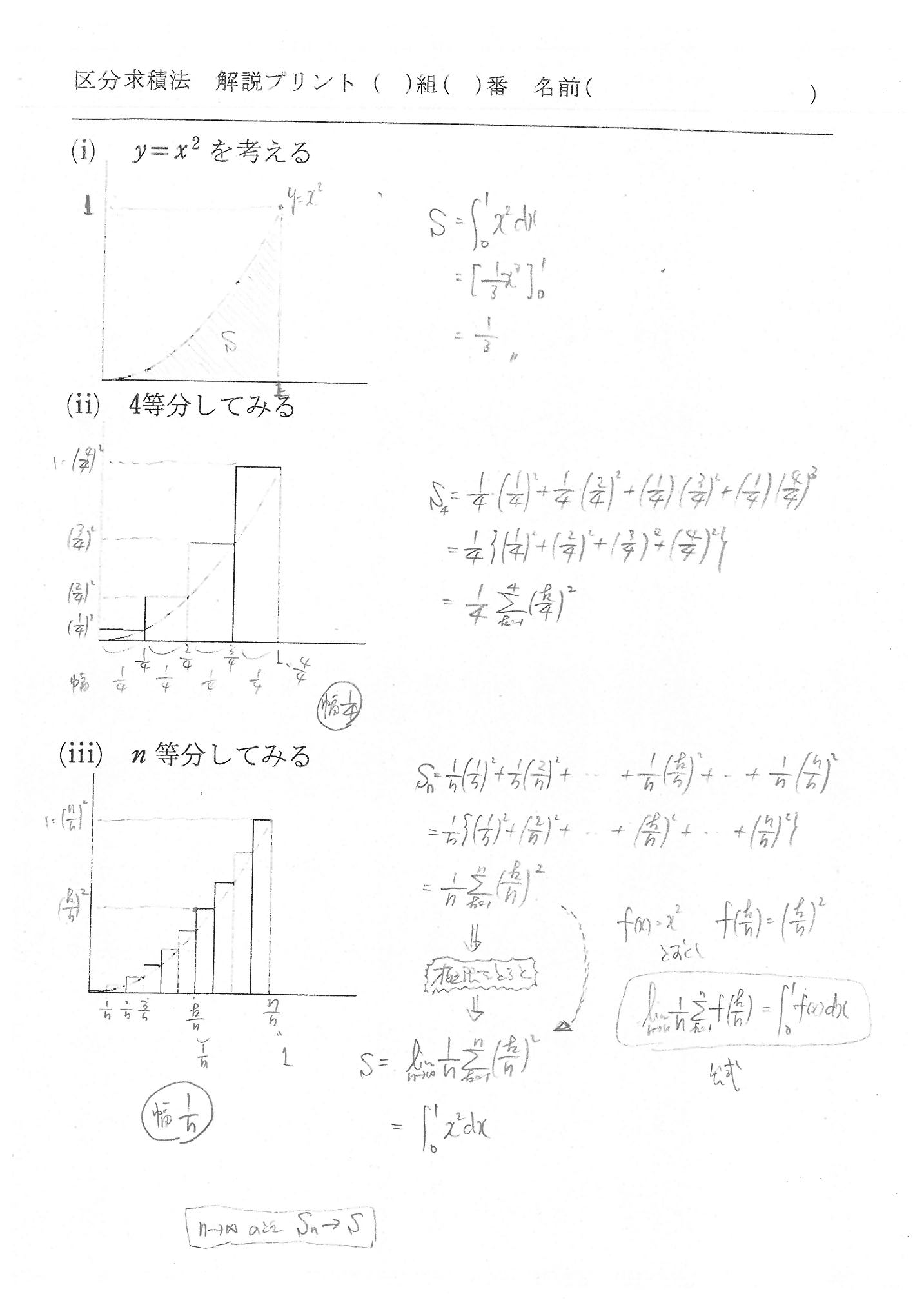
| ↓ こんな感じの解説プリントを作りました。 | 解説プリント原稿 | |||
 |
|
左と右を 両側から |
|||
 |
最上段左図の拡大図
下側から近似してゆく |
|||
 |
最上段右図の拡大図
上側から近似してゆく |
|||
|
この右側の原稿は,授業で活用できるプリントです。印刷してご利用下さい。⇒ |
解説・配布用プリント原稿 | |||
| 2014.11.10追記 この右側の原稿は,更に授業で使いやすく作り直しました。⇒ | 解説プリント原稿PDF | |||
| ↓ こんな感じの解説プリントを作りました。 | 解説プリント原稿 | |||
 |
|
区分求積法とは,積分の定義そのものである。 積分とは微分の逆と解説を受けることが高校数学の常であるが,積分は無限数列の和で表現されると解釈するならば,積分には積分独自の定義が存在し,むしろ微分が積分の逆と捉えることも可能である。 上の図は,面積を上側や下側から近づけてゆくと,どちらも同じある極限に収束するということを図示したものである。横のある一定の範囲をn等分して,曲線上に端点を持つ矩形を作り,n→∞とするならば,それが本来ならば求めにくいはずの,曲線に囲まれた部分の面積になると言うことが理解できると思われる。 上の図を式に変えると,下のようになる。
|
|
今回もBASICで書いてしまった。サンプルプログラムを載せておく。 10 for n=1 to 30 |