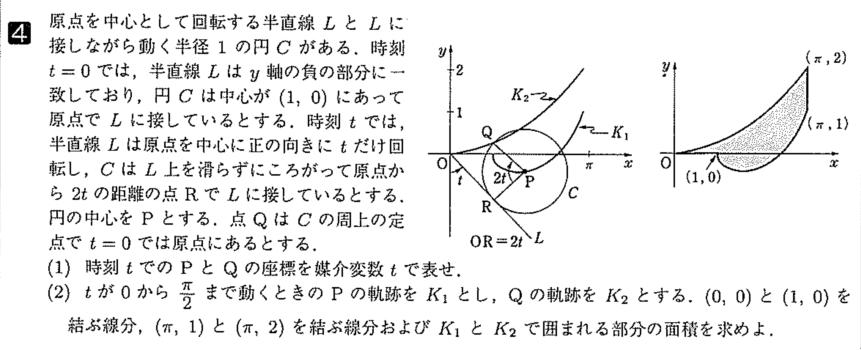
不勉強で，問題自体の存在を知らなかったが，東北大学ではこんな面白い問題を出題されている。

問題文を見ると，完成された図がキレイに掲載されているため，イメージ力の問題ではなく，実際の計算力を見る問題になっている。しかし，本質的なことは文章からこの図を作り出すことにあるのではないかと感じた次第である。

ということで，その動きあるアニメがコレだ・・・

裏読みになるが，本当は東北大学の教授大先生らも，文字だけで出題されたかったのではないだろうか？しかし，そんなことをすると余計なエネルギーが必要となり，ひょっとすると正答率がグッと下がるため，仕方なしに「図までかいてあげようか？おまけで。」ってことになった気がする。

さてさて，前置きはこれぐらいにして，きっかけは，某予備校某先生もおっしゃられていたとおり
　　　「転がる，べたつく，同じ長さ」
ということに尽きるのだろう。回転体の面積や長さの問題として，サイクロイド問題は頻出であるが，その転がる問題も，滑らず転がるという点は共通である。
つまり，
　　　「滑らず転がる＝ペンキがべたつく＝剥がれて張り付く＝同じ長さ」
という視点である。まさにその通りであろう。図の太線部分は同じ長さなので，ベクトル的な表記が座標を決定し，長さがパラメータ表示されるわけである。

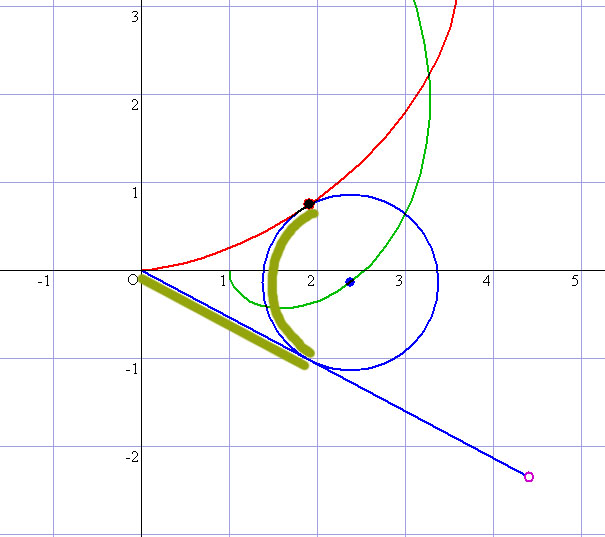
詳細な解答は，PDFファイルをご覧戴くとして，実際に動き，２点が面白いカーブを描くところがこの問題の醍醐味で，さらに面積も変な形だがキレイな結果になるところが意外性がある。

余談になるが，このアニメ図を描きながら，小学生のころのこんな遊びを思い出した。ボール遊びをしていて，肩からボールを腕に沿って転がしながら手でつかむ様な他愛のない遊びである。ボールと腕との複雑な動きが，理想化すると，このような腕（半直線）の上に，滑らず転がるバレーボール（円）の動きそのものである。もし，出題・作問された教授大先生がこのようなことを思い出しながら作成されているのであったら，遊びは学びであるということを実現された，超偉大な問題に見えてくる。

このアニメの元となったGRAPESファイルはこちらからどうぞ。